Théorème de Napoléon
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Vuze49
- Membre Naturel
- Messages: 89
- Enregistré le: 26 Fév 2009, 17:24
-
 par Vuze49 » 20 Mai 2009, 16:15
par Vuze49 » 20 Mai 2009, 16:15
Bonjour j'ai une question sur une des démonstrations possibles du théorème de Napoléon (voir
ici )
Ma question n'est pas sur la démonstration avec les complexes qui est proposée ici, mais avec la démonstration qui utilise des isométries.
J'ai une démo où l'on dit (avec les notations de la figure)

où
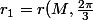,r_2=r(N,\frac{2 \pi}{3}),r_1=r(L,\frac{2 \pi}{3}))
donc MNL est équilatéral.
Je ne comprends pas pourquoi

implique LMN équilatéral.
Merci

-
fourize
- Membre Rationnel
- Messages: 563
- Enregistré le: 26 Oct 2008, 00:40
-
 par fourize » 20 Mai 2009, 16:48
par fourize » 20 Mai 2009, 16:48
bonjour;
Vuze49 a écrit:Bonjour

où
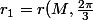,r_2=r(N,\frac{2 \pi}{3}),r_1=r(L,\frac{2 \pi}{3}))
donc MNL est équilatéral.
Je ne comprends pas pourquoi

implique LMN équilatéral.
Merci
fait un dessin et tu verra par composition de rotation que tu revient au
point de depart :++:
* In God we trust, for all others bring data *
-
Vuze49
- Membre Naturel
- Messages: 89
- Enregistré le: 26 Fév 2009, 17:24
-
 par Vuze49 » 20 Mai 2009, 18:11
par Vuze49 » 20 Mai 2009, 18:11
Mon problème c'est pas de montrer que

, ça c'est bon, c'est de savoir pourquoi

implique que le triangle est équilatéral....
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 20 Mai 2009, 21:14
par Doraki » 20 Mai 2009, 21:14
r1 o r2 o r3 = Id <=> r3 = (r2 o r1)^-1.
Donc il n'y a qu'une seule manière de choisir le point L en fonction de M et N pour avoir r1 o r2 o r3 = Id, c'est en prenant L = le centre de r2 o r1.
Comme on sait que en prenant L tel que MNL est équilatéral comme il faut alors r1 o r2 o r3 = Id, ben on a donc trouvé le centre de r2 o r1, qui est le seul endroit possible pour L.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités