Bonjour , j'ai l'énoncé suivant et je suis bloqué à la fin , pourriez vous m'éclairer s'il vous plaît ?
On considère le problème suivant : min [ (x-3/2)²+ (x2-t)²]
sc 1-x1-x2>=0
1-x1+x2>=0
1+x1-x2>=0
1+x1+x2>=0
avec t un paramètre . pour quelles valeurs de t le point x*=(1,0)^T satisfait les conditions KKT ?
Le gradient de F par rapport à x1 , x2 : 2(x1-3/2); 2(x2-t) les dérivées des contraintes :
gradient H1 : (1,1) H2 : (1,-1) H3 : (-1,1) H4 : (-1,-1)
Donc normalement d'après KKT , c'est : 2(x1-3/2)-mu-mu2+mu3+mu4 2(x2-t) -mu1+mu2-mu3+mu4
avec mu1*h1(x1,x2)=0 mu2*h2(x1,x2)=0...
et les mui=(i) de 1à4<=0
Comme système j'aboutis à :
2t=mu1-mu2 -3-mu1+mu2=0 , d'après le système KKT .
Ensuite, que dois-je faire ? Est ce que je dois exprimer t en fonction des mu1 et mu2 . j'ai un t=-3/2 et donc mu2 =0 et mu1=-3 ?
Mais il faut plusieurs valeurs de t donc je ne sais pas comment continuer.
Merci.
Théorème karush khun tucker (KKT)
6 messages
- Page 1 sur 1
C'est  ou
ou  dans la fonction objectif ?
dans la fonction objectif ?
Ta essayé de faire comme là ? : http://www.maths-forum.com/optimisation-non-lineaire-155460.php
Ta essayé de faire comme là ? : http://www.maths-forum.com/optimisation-non-lineaire-155460.php
[CENTER] \ \ : \ \ \left\{\begin{array}{lrr} min \ \ \ z & = & {x_1}^2 + {x_2}^2 - 3x_1 - 2x_2t + t^2 + \frac{9}{4}\\ s.c. \\ & & x_1 \ \ + \ \ x_2 \ \ - \ \ 1 \ \ \le \ \ 0 \\ & & x_1 \ \ - \ \ x_2 \ \ - \ \ 1 \ \ \le \ \ 0 \\ & & - \ \ x_1 \ \ + \ \ x_2 \ \ - \ \ 1 \ \ \le \ \ 0 \\ & & - \ \ x_1 \ \ - \ \ x_2 \ \ - \ \ 1 \ \ \le \ \ 0 \\ & & x \ \ \ge \ \ 0 \end{array}\right.) [/CENTER]
[/CENTER]
Si je reprend les conditions de KKT :
[CENTER]Stationarity
 [/CENTER]
[/CENTER]
[CENTER]Complementary slackness[/CENTER]
[CENTER] & = & 0\\ \mu_2 & (& & x_1 & - & x_2 & - & 1 ) & = & 0\\ \mu_3 & (& - & x_1 & + & x_2 & - & 1 ) & = & 0\\ \mu_4 & (& - & x_1 & - & x_2 & - & 1 ) & = & 0 \end{array}\right.)
[/CENTER]
[CENTER]Dual feasibility[/CENTER]
[CENTER] [/CENTER]
[/CENTER]
Pour le point :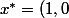^T) on a :
on a :
[CENTER]Complementary slackness :
Stationarity :
Dual feasibility : [/CENTER]
[/CENTER]
La condition est donc :
Si je reprend les conditions de KKT :
[CENTER]Stationarity
[CENTER]Complementary slackness[/CENTER]
[CENTER]
[/CENTER]
[CENTER]Dual feasibility[/CENTER]
[CENTER]
Pour le point :
[CENTER]Complementary slackness :
Stationarity :
Dual feasibility :
La condition est donc :
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
