Optimisation non linéaire (résolu)

[Raven]

Bonjour , j'ai un exercice où je doute , je voudrais avoir des précisions...

Voilà le sujet:
Pour la 1) j'ai fait le graph
2) oui car la matrice hessienne est positive donc il y a au plus une solution et comme la fonction est coercive ,il y en a au moins une .
(Je sais pas du tout si c'était comme ça qu'il fallait justifier)

3) On peut écrire KKT car ce sont des contraintes linéaires?
4) j'obtiens : 4x1+2x2-20+(mu1)-(mu2)-5(mu3)=0
2x14x2-28-(mu1)-(mu2)-(mu3)=0
avec mu1 mu2 et mu3 plus petit ou égal à 0
et (mu1)*(-x1+x2-5)=0
(mu2)*(x1+x2-7)=0
(mu3)(5x1+x215)=0

5)je n'ai pas réussi cette question . Doit on remplacer x1 et x2 par ces points ?

6) matrice hessienne :
(4 2
2 4)

les valeurs propres sont positives , donc la matrice est semi définie positive ?

7) je bloque aussi...


Merci de m'aider si vous pouvez !

http://www.hostingpics.net/viewer.php?id=340515exopartielopti.jpg

[Cliffe]

C'est plutôt "Optimisation non linéaire" le titre ...

[Cliffe]

Je vais essayé d'aider un peu, mais je n'ai jamais fait d'optimisation non linéaire et encore moins de KKT :p.

1.

On note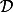 le domaine de réalisabilité.

[CENTER] [/CENTER]

2.

Solution : Oui, F est définie sur donc le problème admet une solution.

Solution réalisable : Oui il existe une solution réalisable (et même une infinité) car le domaine de réalisabilité n'est pas vide : et la fonction F est bien définie sur .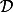

Solution optimale : F est borné sur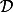 donc le problème admet une solution optimale.

3.

Je ne sais pas :triste:

4.

D'après wikipédia :
[CENTER]Stationarity [/CENTER]
[CENTER]

[CENTER]Complementary slackness[/CENTER]


Dual feasibility
[/CENTER]

5.

Pour :

[CENTER]On remplace dans le 2ème système :

On remplace dans le premier système : [/CENTER]

[CENTER]Donc, impossible pour car on ne respecte par la condition de Dual feasibility[/CENTER]

Pour :

[CENTER]Même raisonnement, on trouve : [/CENTER]

[CENTER]Le système est vérifié pour [/CENTER]

6.

Je vois pas trop le rapport entre l'opérateur Laplacien et la matrice hessienne, m'enfin :

[CENTER]

Valeur propres : [/CENTER]

Donc est une matrice définie positive.

7.

[CENTER]D'après 5, 6 et 7, la solution optimale est : [/CENTER]

[Raven]

Merci beaucoup pour ta réponse .
Pour la question 4) . Quand on remplace dans le deuxième système c'est pas plutôt (mu1)*0=*0 au lieu de -12*(mu1)?
Aussi , je ne sais plus comment on détermine les valeurs propres , pour moi c'était les valeurs de la diagonale , mais apparemment non...

[Raven]

J'ai un autre exercice aussi d'optimisation linéaire qui est assez complexe .
http://www.hostingpics.net/viewer.php?id=167364opti3.jpg

En fait pour la question je crois que c'est le sytème en rajoutant des variables x4 , x5 et x6 et mettre des égals à la place des inégalités ?

pour la 2) je bloque

pour la 3) c'est max f(x) sc ax=b avec x>0 ?

je bloque ensuite , je ne sais pas si il faut utiliser le simplexe ou pas...

[Cliffe]

Merci beaucoup pour ta réponse .
Pour la question 4) . Quand on remplace dans le deuxième système c'est pas plutôt (mu1)*0=*0 au lieu de -12*(mu1)?

Exact, j'ai mis un - ^^, j'utilise un logiciel pour résoudre les systèmes et pour les valeurs propres.
J'ai corrigé.

[Raven]

D'accord merci.

[Cliffe]

[CENTER] [/CENTER]

avec et on note , .

1. Forme standard :

[CENTER] [/CENTER]

avec les variables d'écarts.

2.

Soit la base et on note la matrice associer. Deux manières de justifier qu'elle n'est pas réalisable.

1er méthode : Les variables hors base prennent une valeur nulle. On se retrouve donc avec la contrainte 2 : , or . Donc n'est pas réalisable.

2ème méthode : On revient à la définition de base réalisable : une base est réalisable si elle est valide (Voir la définition de base valide) et si elle permet d'affecter des valeurs admissibles aux variables en base. Il faut donc vérifier que (base valide) et .

[CENTER] [/CENTER]

- donc est valide.
- , donc n'est pas réalisable.

3.

L'astuce de la méthode en deux phases consiste à ajouter des variables de base «artificielles» dans les équations où il n'y a aucune variable candidate naturelle. Ajoutons la variable artificielle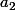 dans la deuxième contrainte (car le second membre est négatif) et on remplace la fonction objectif :

[CENTER] [/CENTER]

On résout ensuite en utilisant le formalisme du dictionnaire :

[CENTER] [/CENTER]

Premier pivotage : entre en base, on cherche alors la variable sortante :

[CENTER] [/CENTER]

C'est donc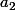 qui va s'annuler et sortir de base. On réécrit le système :

[CENTER] [/CENTER]

Tous les coûts réduit sont nul. La base est réalisable. On peut donc passer à la résolution classique, puisqu'on dispose d'une base réalisable.

4.

On a démontrer dans la question 3 qu'il s'agit bien d'une base réalisable.

On re-vérifie :
- : donc base valide
- : donc base réalisable.

5.

[CENTER] [/CENTER]

6.

[CENTER] [/CENTER]

Je ne comprend pas votre manière de construire votre tableau, je fait comme ça moi :

[CENTER] [/CENTER]

7.

A toi de résoudre à ta manière.

8.

[CENTER] [/CENTER]

avec et on note .

9.

On note les variables d'écart du dual.

Complémentarité :
De plus, on sait qu'à l'optimal on a :

On résout alors le système :

Dis moi si y'a des erreurs :id:

[Raven]

Merci beaucoup :)
Mais j'ai plein de questions...

Tout d'abord question 1) : quand on met sous forme standard , on doit obligatoirement passer au max?
pour la question 2 , quand vous faites B^-1b ? c'est 4 à la place de 7 non ?

pour la 2) pourquoi c'est x1 qui entre en base ?
Donc vu que c'est x1 la variable entrante , les autres sont nulles?
Ensuite vous faites sortir a2 je comprends pas .
En fait j'ai toujours fait la méthode su simplexe avec le tableau , est ce que c'est ça que vous faites ?

pour la question4): ils disent de résoudre le système avec les contraintes , mais vous réutilisez le fait que la base est réalisable ça fonctionne quand même ?
Et dans la question 3 , on a démontré que c'était la base (s1,x1,s3) qui était réalisable , pas (3,1,5) ?

Pour les 5 et 6 ) je comprends pas comment vous obtenez cette fonction objectif et le vecteur des coûts réduits . C'est pas en fonction de x1 et x2 donc (0,1)?

Pour la question 9) les conditions de complémentarité c'est toujours celles là , je les aies avaient jamais vue dans la résolution d'un dual .
et le w*=z* tu l'obtient de où ?

Pour la question 10 que tu n'as pas traité , je voulais savoir si la nouvelle solution optimale sera y1= alpha , y2= 2+alpha et y3= 1+alpha ?

Désolé pour toutes ces questions...mais c'est pour mieux comprendre , sinon ça sert à rien :)

Merci !

[Cliffe]

Tout d'abord question 1) : quand on met sous forme standard , on doit obligatoirement passer au max?

C'est la définition de la forme standard oui.

pour la question 2 , quand vous faites B^-1b ? c'est 4 à la place de 7 non ?

Oui c'est un 4, on multiplie par la matrice identité, erreur de frappe.

pour la 2) pourquoi c'est x1 qui entre en base ?

C'est la question 3 non ?
x1 entre en base car sont coût réduit est posiftif.

Donc vu que c'est x1 la variable entrante, les autres sont nulles?

Les variables hors base sont nulles.

Ensuite vous faites sortir a2 je comprends pas.

C'est l'idée du simplexe. A chaque itération, on se déplace sur le polyèdre des contraintes.
Comment ? En augmentant (car on maximise) la valeur d'une variable (ici x1) jusqu'à une certaine limite (et oui le problème est bornée :lol3:).
Cette limite est donnée par une des contraintes du problème (on doit chercher laquelle). Et donc, quand x1 augmente, une variable en base va s'annuler, ici c'est a2.

En fait j'ai toujours fait la méthode su simplexe avec le tableau , est ce que c'est ça que vous faites ?

J'ai jamais fait de simplexe perso. Quel études fais tu ?

pour la question4): ils disent de résoudre le système avec les contraintes , mais vous réutilisez le fait que la base est réalisable ça fonctionne quand même ?

J'ai démontrer dans 3) quel été réalisable (même si ce n'est pas demandé) et ensuite je vérifie le système des contraintes avec . Tu peux aussi remplacer les valeurs dans le système si tu veux :id:

Et dans la question 3 , on a démontré que c'était la base (s1,x1,s3) qui était réalisable , pas (3,1,5) ?

Ton prof doit surement noter les variables . Moi je note les variables d'écart pour bien faire la différence. Ensuite il note base comme un ensemble d'incide :mur: normalement une base c'est un ensemble de variables, m'enfin ... donc si tu note le vecteur de toutes les variables et que tu construit la base avec les variables 3 1 et 5 tu obtiens bien :

Pour les 5 et 6 ) je comprends pas comment vous obtenez cette fonction objectif et le vecteur des coûts réduits . C'est pas en fonction de x1 et x2 donc (0,1)?

Regarde la forme standard du problème. Tu as . On cherche en fonction des variables hors base. Tu utilise la deuxième contrainte pour sortir . Soit et tu remplace dans l'expression de .

Pour la question 9) les conditions de complémentarité c'est toujours celles là , je les aies avaient jamais vue dans la résolution d'un dual.

J'ai taper sur le net et tu as des exemples :lol3:

et le w*= z* tu l'obtient de où ?

C'est l’intérêt du dual, il sert a ça. On résout le dual pour connaître la valeur optimal du primal. Le dual à une utilité, on ne s'amuse pas à le calculer pour rien ^^

Pour la question 10 que tu n'as pas traité , je voulais savoir si la nouvelle solution optimale sera y1= alpha , y2= 2+alpha et y3= 1+alpha ?

Tu dois regarder des cours de : Postoptimalité et Analyse de sensibilité. Si j'ai le temps je regarderais un autre jours.

[Raven]

D'accord .
Mais pour la question 3
Comment vous savez que les coûts réduits sont positifs. Parce que d'habitude on voit ça dans le tableau sur la ligne "c"mais là vu qu'on fait sous forme dictionnaire je ne vois pas.

Pour le coût réduit de la question 6 . J'ai compris ce que vous avez fait . Mais le -1 je
voispas d'où il vient . C'est pas le coef de x2 donc 1 ?

Pour la construction du tableau. C'était donné comme ça . On fait comme ça d'habitude. Et ensuite on met la ligne des c . Mais m'a vu que c'est (1,-1) . Je dois mettre 1 en x1 -1 en x2 et les autres des zéro ? J'ai essayé mais ça fonctionne pas
Je suis en licence mathématique appliquées aux sciences sociales...

[Cliffe]

Mais pour la question 3
Comment vous savez que les coûts réduits sont positifs. Parce que d'habitude on voit ça dans le tableau sur la ligne "c"mais là vu qu'on fait sous forme dictionnaire je ne vois pas.

On a . On cherche a maximizer . On veux augmenter une des variables hors base (, ou ). Si j'augmente ou , va diminuer, car leur coefficient sont négatif. est la seul variable hors base qui a un coefficient positif (+1), donc on va augmenter , ce qui signifie que "entre en base". Les coefficients dont je parle sont appelés "coût réduit". Lorsqu'ils sont tous négatif, on ne peut plus augmenter et donc l'algorithme est terminer.

Pour le coût réduit de la question 6 . J'ai compris ce que vous avez fait . Mais le -1 je
voispas d'où il vient . C'est pas le coef de x2 donc 1 ?

Coût réduit des variables hors base, tjr pareil. Les coefficients de et .

Pour la construction du tableau. C'était donné comme ça . On fait comme ça d'habitude. Et ensuite on met la ligne des c . Mais m'a vu que c'est (1,-1) . Je dois mettre 1 en x1 -1 en x2 et les autres des zéro ? J'ai essayé mais ça fonctionne pas.

Je connais pas trop la forme tableau, je préfère la forme dictionnaire.



Pour le , il s'agit du théorème de Dualité forte.

[Raven]

Ohhhh sayé je crois que j'ai compris !
Juste une dernière question . Quand on a pris une valeur artificielle au niveau de la 2ème contrainte parce que -2<0 . Mais est ce qu'on Peut avoir deux contraintes négatives ? Et dans ce cas on doit mette le -a2?

[Raven]

pour la dualité forte et son théorème , on ne l'a pas dans le cours c'est bizarre...mais bon tant pis .
Merci beaucoup :)