Théorème des 4 sommets!

[fourize]

bonjour!

j'ai exercice sous la main auquel je comprends mais la question me parait évident et du coup, je ne vois pas du tout ce qu'il faut faire:

soient a > b > 0 et l'ellipse données par (a*cost, b*sint)
le grand axe de l'ellipse, coupe l'ellipse en deux points. Vérifier que ces deux points sont des sommets de l'ellipse.

je sais tout simplement que ces sommets sont A(a,0) et A'(-a,0) puisque a>b,
si quelqu'un peu m'aider à vérifier que ces deux points sont des sommets de l'ellipse.

cordialement,

[Pythales]

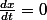
Peut-être aux sommets ?

[fourize]

re,

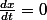
Peut-être aux sommets ?

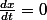
supposons que c'est le cas: je touve t= 0 ou . en remplaçant ces valeurs en x, je trouve A et A'. mais pourquoi pas ?????

au passage, j'ai un autre exo bizarre:

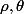
soit a>0, et la courbe parametrée en cordonnées polaires () par
*montrer que le parametrage est régulier si et seulement si a 1

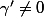
je sais que le parametrage est regulier si , en derivant par rapport à le a devient 0 .
:help: :help: :help: :help: :help: :help: :help: :help: :help: :help:

[fourize]

j'ai fini par trouver une solution pour ce sujet tout seul !

pour les interressé envoyé moi un mail ou un MP .