Nombre de sommets d'une intersection

[Sylviel]

Pour le coup je ne savais pas trop où poster...

Est-ce que l'intersection d'un pavé de R^n avec un hyperplan a au plus n+1 points ?

En vérité il s'agit d'un pavé (droit) du cadran positif (R+)^n ayant pour sommet 0, et du simplexe (celui dont la somme des coeff vaut 1), mais je ne pense pas que cela change grand chose...

Et une démo, si quelqu'un a ça ?

[Ben314]

Salut,
Je comprend pas trop ton histoire de "pavé" : si je prend un cube de R^3 et que je le coupe par un plan,
Soit on parle de cube plein (0Soit on parle des faces du cube (la frontière du "cube plein") et l'intersection est un polygône contenant... une infinité de point.
Soit ce que tu appelle pavé désigne un ensemble d'arrêtes (de dimension 1), mais dans ce cas, ça me fait un peu bizare de parler de "pavé" pour désigner une réunion de segments.

Donc... à clarifier...

P.S. : tu serait pas en train de faire de l'homologie simpliciale par hasard ?

[Sylviel]

Oui, désolé j'étais pas clair : c'est pas points, c'est sommets ;-)

Je fais de l'optimisation stochastique (en l'occurrence on parle de mesures de risques) et au détour de calcul je trouve un ensemble de contraintes toutes simples : entre 0 et une borne (donc un pavé plein, ie un produit cartésien) et qui doivent être des probas (donc qui somme à 1). Un rien d'optimisation linéaire dit qu'il suffit de maximiser sur les sommets d'un polyhèdre convexe (fonction objectif linéaire), et je voulais estimer leur nombre, donc je sors un peu de mon domaine habituel...

[Ben314]

De toute façon, rien que dans R^3, si tu coupe un cube "en biais" en passant par le milieu de certaines arrêtes (fait un dessin sur un papier, ça ira plus vite que si je le fait sur l'ordi...), tu obtient un joli hexagone régulier.
Comme 6>3+1, ta "borne" de n+1 n'est pas valable.

P.S. Tu n'as pas d'hypothéses sur les longueurs des cotés de ton pavé ?

[Sylviel]

Non je n'ai pas d'hypothèses (enfin pas des simples, et peu contraignantes : c'est , où 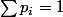, et alpha dans ]0,1[ ). En même temps la valeur de la borne n'est pas fondamentale. Par contre je n'avais pas vu l'hexagone... :$

Bon, une idée de borne alors ?

[Ben314]

Je vient de faire un petit calcul dans le cas d'un "hypercube" de coté 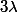et je trouve que le nombre de sommets est (coeff binomial) où est la partie entière de .
Le "max" est donc lorsque p est environ égal à (n-1)/2 et il est... assez grand si n est grand...

Dans le cas d'un pavé quelconquue, je sais pas, mais j'intuiterais que le max est obtenu pour un hypercube (?)

[Sylviel]

Merci pour l'indication... Comment as-tu fais le calcul ?

[Ben314]

L'équation d'une arrête de l'hypercube est de la forme :
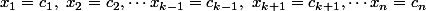et
où les différentes constantes sont soit soit ( il y a donc arrêtes)
Une telle arête coupe l'hyperplan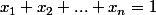 ssi il existe tel que 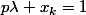où est le nombre de égaux à .
Ce qui équivaut à c'est à dire à et donc à 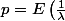(en supposant 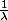non entier, c'est à dire en supposant que l'hyperplan ne passe par aucun sommet de l'hypercube)
Enfin, le nombre d'arête telles que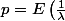 des soient égaux à est