Théorème de Baire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
JackxSummer
- Membre Naturel
- Messages: 17
- Enregistré le: 01 Juin 2015, 14:43
-
 par JackxSummer » 27 Oct 2015, 18:28
par JackxSummer » 27 Oct 2015, 18:28
Est-ce-que le théorème de Baire valable dans un espace topologique quelconque ou seulement dans un espace complet ?.
-
mathelot
 par mathelot » 27 Oct 2015, 18:56
par mathelot » 27 Oct 2015, 18:56
JackxSummer a écrit:Est-ce-que le théorème de Baire valable dans un espace topologique quelconque ou seulement dans un espace complet ?.
d'après le wiki, on peut supposer "localement compact".
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
 par MouLou » 27 Oct 2015, 19:25
par MouLou » 27 Oct 2015, 19:25
Non il y'en a d'autres, d'ailleurs on parle d'espace de Baire lorsque la propriété de Baire est vérifiée :).
Les espaces complet sont donc des espaces de Baire
-
JackxSummer
- Membre Naturel
- Messages: 17
- Enregistré le: 01 Juin 2015, 14:43
-
 par JackxSummer » 27 Oct 2015, 19:44
par JackxSummer » 27 Oct 2015, 19:44
Parce-que qlq ouvrages supposent que l'espace topologique soit complet mais dans la démonstration la complétude n'est pas utilisée.
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
 par MouLou » 27 Oct 2015, 20:22
par MouLou » 27 Oct 2015, 20:22
JackxSummer a écrit:Parce-que qlq ouvrages supposent que l'espace topologique soit complet mais dans la démonstration la complétude n'est pas utilisée.
La preuve la plus classique utilise la complétude en introduisant une suite de Cauchy. De quel ouvrage parle tu par exemple?
-
JackxSummer
- Membre Naturel
- Messages: 17
- Enregistré le: 01 Juin 2015, 14:43
-
 par JackxSummer » 27 Oct 2015, 20:35
par JackxSummer » 27 Oct 2015, 20:35
MouLou a écrit:La preuve la plus classique utilise la complétude en introduisant une suite de Cauchy. De quel ouvrage parle tu par exemple?
Bernard Aupetit, A Primer on Spectral Theory.
Jacques Dixmier, General Topology.
Fred H. Croom, Principles of Topology.
Gerard Buskes & Arnoud van Rooij, TOPOLOGICAL SPACES From Distance to Neighborhood.
etc...
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
 par MouLou » 27 Oct 2015, 21:06
par MouLou » 27 Oct 2015, 21:06
J'ai regardé le Diximer, il utilise la complétude via le théorème des fermés emboités non?
-
JackxSummer
- Membre Naturel
- Messages: 17
- Enregistré le: 01 Juin 2015, 14:43
-
 par JackxSummer » 27 Oct 2015, 21:35
par JackxSummer » 27 Oct 2015, 21:35
MouLou a écrit:J'ai regardé le Diximer, il utilise la complétude via le théorème des fermés emboités non?
Il a dit:
Let

be a complete metric space,
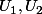
,... a sequence of dense open subsets of

. Then

· · · is dense in

.
-
JackxSummer
- Membre Naturel
- Messages: 17
- Enregistré le: 01 Juin 2015, 14:43
-
 par JackxSummer » 27 Oct 2015, 21:42
par JackxSummer » 27 Oct 2015, 21:42
MouLou a écrit:J'ai regardé le Diximer, il utilise la complétude via le théorème des fermés emboités non?
Oui, il utilise le théorème des fermés emboités.
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
 par MouLou » 27 Oct 2015, 21:59
par MouLou » 27 Oct 2015, 21:59
La complétude est donc belle et bien utilisée. Avec les fermés emobités tu as besoin de la complétude. Tu peux a la rigueur t'en défaire si tes fermés sont convexes.
Peut etre alors localement convexe peut marcher mais je peux pas trop dire de plus, wiki sait surement mieux
-
JackxSummer
- Membre Naturel
- Messages: 17
- Enregistré le: 01 Juin 2015, 14:43
-
 par JackxSummer » 27 Oct 2015, 22:05
par JackxSummer » 27 Oct 2015, 22:05
MouLou a écrit:La complétude est donc belle et bien utilisée. Avec les fermés emobités tu as besoin de la complétude. Tu peux a la rigueur t'en défaire si tes fermés sont convexes.
Peut etre alors localement convexe peut marcher mais je peux pas trop dire de plus, wiki sait surement mieux
Mais est-ce-que possible de la démontrer sans la notion de complétude, seulement par les voisinages.?
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
 par MouLou » 27 Oct 2015, 22:17
par MouLou » 27 Oct 2015, 22:17
Tu reprends la même démo je pense: A l'intersection des ouverts, O un ouvert de E, alors tu veux montrer que
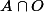
est non vide: alors par densité de
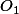
tu trouves x dans
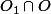
, ET LA, au lieu de prendre une boule fermée, tu prends un voisinnage compact inclus dans
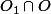
(ouvert), et rebelotte. La ou ça va marcher c'est que l'intersection de compacts est compact et t'auras une suite d'un compact qui aura une valeur d'adhérence. Donc l'intersection sera non vide
Pour la preuve propre tu peux voir Queffelec, Topologie
-
JackxSummer
- Membre Naturel
- Messages: 17
- Enregistré le: 01 Juin 2015, 14:43
-
 par JackxSummer » 27 Oct 2015, 22:22
par JackxSummer » 27 Oct 2015, 22:22
MouLou a écrit:Tu reprends la même démo je pense: A l'intersection des ouverts, O un ouvert de E, alors tu veux montrer que
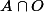
est non vide: alors par densité de
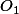
tu trouves x dans
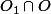
, ET LA, au lieu de prendre une boule fermée, tu prends un voisinnage compact inclus dans
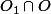
(ouvert), et rebelotte. La ou ça va marcher c'est que l'intersection de compacts est compact et t'auras une suite d'un compact qui aura une valeur d'adhérence. Donc l'intersection sera non vide
Pour la preuve propre tu peux voir Queffelec, Topologie
On n'a pas le droit d'utiliser la notion de boule si on est dans un espace topologique quelconque. (C'est mon cas)
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
 par MouLou » 27 Oct 2015, 22:38
par MouLou » 27 Oct 2015, 22:38
JackxSummer a écrit:On n'a pas le droit d'utiliser la notion de boule si on est dans un espace topologique quelconque. (C'est mon cas)
Je prends pas de boule, je prend un voisinage compact, j'ai le droit
-
JackxSummer
- Membre Naturel
- Messages: 17
- Enregistré le: 01 Juin 2015, 14:43
-
 par JackxSummer » 27 Oct 2015, 22:48
par JackxSummer » 27 Oct 2015, 22:48
Oui j'ai comprend, par exemple, pour
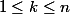
,
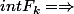
soit
)
on a,
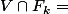
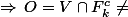
on a

ouvert, donc soit
)
tel que
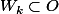
et on construit une suite de voisinages de
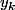
telle que
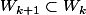
, et on fait l'intersection, on trouve
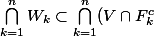=V\cap (\bigcap_{k=1}^{n} F_k^{c} )\neq\empty)
, et par passage au complémentaire, on trouve
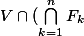=\empty)
, ce qui donne,
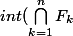=\empty)
????????
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
 par MouLou » 27 Oct 2015, 23:03
par MouLou » 27 Oct 2015, 23:03
je ne comprends pas ta première affirmation: soit
)
on a,
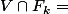
, x est au moins dans l'intersction, puis même, a la rigueur il existerait un voisinnage, et puis même interieur non vide ne signifie que tous les points sont isolés
-
JackxSummer
- Membre Naturel
- Messages: 17
- Enregistré le: 01 Juin 2015, 14:43
-
 par JackxSummer » 27 Oct 2015, 23:13
par JackxSummer » 27 Oct 2015, 23:13
MouLou a écrit:je ne comprends pas ta première affirmation: soit
)
on a,
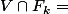
On dit que

est intérieur à

si il existe un voisinage

de

(on prend par exemple un voisinage ouvert) tel que

soit contenu dans

. Si
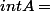
ceci donne, quelque soit
)
(voisinage ouvert de x):
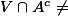
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
 par MouLou » 27 Oct 2015, 23:18
par MouLou » 27 Oct 2015, 23:18
JackxSummer a écrit:On dit que

est intérieur à

si il existe un voisinage

de

(on prend par exemple un voisinage ouvert) tel que

soit contenu dans

. Si
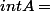
ceci donne, quelque soit
)
(voisinage ouvert de x):
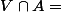
tu vois bien que c'est n'importe quoi, x est dans l'intersection deja...
-
JackxSummer
- Membre Naturel
- Messages: 17
- Enregistré le: 01 Juin 2015, 14:43
-
 par JackxSummer » 27 Oct 2015, 23:31
par JackxSummer » 27 Oct 2015, 23:31
MouLou a écrit:tu vois bien que c'est n'importe quoi, x est dans l'intersection deja...
Oui, je la corrigée.
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
 par MouLou » 27 Oct 2015, 23:38
par MouLou » 27 Oct 2015, 23:38
Hmm comment tu justifies que l'intersection des Wk est non vide? c'est la qu'il faut les prendre compacts je pense
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
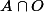 est non vide: alors par densité de
est non vide: alors par densité de 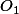 tu trouves x dans
tu trouves x dans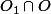 , ET LA, au lieu de prendre une boule fermée, tu prends un voisinnage compact inclus dans
, ET LA, au lieu de prendre une boule fermée, tu prends un voisinnage compact inclus dans 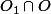 (ouvert), et rebelotte. La ou ça va marcher c'est que l'intersection de compacts est compact et t'auras une suite d'un compact qui aura une valeur d'adhérence. Donc l'intersection sera non vide
(ouvert), et rebelotte. La ou ça va marcher c'est que l'intersection de compacts est compact et t'auras une suite d'un compact qui aura une valeur d'adhérence. Donc l'intersection sera non videest non vide: alors par densité de
tu trouves x dans
, ET LA, au lieu de prendre une boule fermée, tu prends un voisinnage compact inclus dans
(ouvert), et rebelotte. La ou ça va marcher c'est que l'intersection de compacts est compact et t'auras une suite d'un compact qui aura une valeur d'adhérence. Donc l'intersection sera non vide
