Termes général d'une suite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 25 Nov 2006, 22:15
par Aspx » 25 Nov 2006, 22:15
Bonjour j'ai une petite question. Je sais calculer le terme général de suites commes
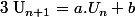
où a et b sont des constantes mais quand ces termes dépendent de n comment faire ?
PS: Ma suite:
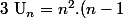!+n.U_{n-1})
(c'est le nombre de surjections de {1,2,...,n+1} vers {1,2,...,n} :we:
Merci d'avance !
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 26 Nov 2006, 09:30
par yos » 26 Nov 2006, 09:30
Bonjour.
Pas de méthode générale.
Dans ton cas particulier, écris les relations les unes sous les autres en faisant varier l'indice k de 1 à n, puis fais une combinaison de ces égalités avec des coefficients convenables.
-
simplet
- Membre Relatif
- Messages: 374
- Enregistré le: 29 Oct 2005, 12:28
-
 par simplet » 26 Nov 2006, 10:01
par simplet » 26 Nov 2006, 10:01
C'est à dire qu'il faut que tu conjectures (que tu essaies de trouver) une formule de recurrence pour ton terme Un (en fonction de U1 inévitablement) (si je ne dis pas de bétise U1=2) puis que tu la démontres , par recurrence, bien entenduuuu.
Personnellement j'ai du aller jusqu'à k=5 pour trouver ma formule de recurrence (je c pas si elle est bonne mais bon), j'ai trouver
Un= n^2. (n-1)+somme(i de 1 à n-2) n! (n-i)^2 + n! U1
En remplacant U1 on peut simplifier un peu,
je ne garantis pas cette mormule!! :we:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 26 Nov 2006, 11:07
par yos » 26 Nov 2006, 11:07
On peut aussi raisonner directement : Pour une telle surjection, il y a n éléments pouvant avoir 2 antécédents, lesquels peuvent être choisis parmi n+1 éléments. Quant aux n-1 éléments restants dans l'ensemble de départ, ils forment une des (n-1)! bijections avec les (n-1 ) éléments restants de l'ensemble d'arrivée.
D'où
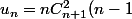!=n!C_{n+1}^2)
.
Ce qui donne
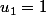
et pas 2.
-
simplet
- Membre Relatif
- Messages: 374
- Enregistré le: 29 Oct 2005, 12:28
-
 par simplet » 26 Nov 2006, 11:30
par simplet » 26 Nov 2006, 11:30
oui,oui U1=1 jss bete, 1 ->1 et 2->1 .
-
simplet
- Membre Relatif
- Messages: 374
- Enregistré le: 29 Oct 2005, 12:28
-
 par simplet » 26 Nov 2006, 11:32
par simplet » 26 Nov 2006, 11:32
et je préfere le calcul direct, on voit mieux ce qu'il se passe
-
simplet
- Membre Relatif
- Messages: 374
- Enregistré le: 29 Oct 2005, 12:28
-
 par simplet » 26 Nov 2006, 11:34
par simplet » 26 Nov 2006, 11:34
simplet a écrit:Un= n^2. (n-1)+somme(i de 1 à n-2) n! (n-i)^2 + n! U1
:we:
devient
Un= n^2. (n-1)+somme(i de 1 à n-1) n! (n-i)^2
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 26 Nov 2006, 13:10
par Aspx » 26 Nov 2006, 13:10
Non mais oui lol, le résultat je le connais mais c'était pas précisemment pour calculer le terme général en lui même.
C'est justement la recherche du terme général d'une suite récurrente non linéaire qui m'interesse, mais en effet il me semble pas qu'il y ai de formules générales. La conjecture suivie de la récurrence reste le meilleur moyen c'est sur.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités