Bonjour à tous, je bloque actuellement sur le développement Mac-Laurin de la fonction suivante :
f(x,y) = sin (x^2 + y^2)
Il m'est demandé de développer la fonction jusqu'à l'ordre 6. Ceci étant dit, j'ai entendu certaines personnes dire que l'on peut modifier la fonction sinus (en logarithme népérien ??) pour ne pas devoir calculer la quinzaine de dérivées partielles.
Merci d'avance pour toutes vos suggestions.
Taylor-Mac Laurin astuce pour ordre très grand
3 messages
- Page 1 sur 1
Salut,
Bon, déjà (et comme d'hab...) il a falu que je cherche quoi c'était le développement de "Mac Laurin" (tout ce qui est nom propres, il n'y a rien qui rentre...) et en fait, c'est le développement limité en 0 (donc ici en (0,0)) ce qui facilite en général grandement les choses...
Ensuite, pour des fonctions de plusieurs variables, le "petit o" de la fin du D.L., c'est un "petit o" en la norme du (petit) vecteur X ce qui fait qu'ici, c'est "fingers in the noze" vu que la fonction ne dépend que de la norme du vecteur (x,y).
Conclusion : le truc que tu cherche, c'est (on ne peut plus bètement) :
=x^2+y^2-\frac{1}{3!}(x^2+y^2)^3+\frac{1}{5!}(x^2+y^2)^5...)
Et, à la limite, si tu veut absolument voir apparaitre tes fameuses dérivées partielles, ben il suffit de développer les^n)
P.S. en plus, vu qu'il te le faut qu'à l'ordre 6 (i.e. uniquement les termes en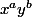 avec
avec 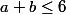 , il suffit de prendre les 2 premiers termes du D.L. de
, il suffit de prendre les 2 premiers termes du D.L. de ) .
.
Bon, déjà (et comme d'hab...) il a falu que je cherche quoi c'était le développement de "Mac Laurin" (tout ce qui est nom propres, il n'y a rien qui rentre...) et en fait, c'est le développement limité en 0 (donc ici en (0,0)) ce qui facilite en général grandement les choses...
Ensuite, pour des fonctions de plusieurs variables, le "petit o" de la fin du D.L., c'est un "petit o" en la norme du (petit) vecteur X ce qui fait qu'ici, c'est "fingers in the noze" vu que la fonction ne dépend que de la norme du vecteur (x,y).
Conclusion : le truc que tu cherche, c'est (on ne peut plus bètement) :
Et, à la limite, si tu veut absolument voir apparaitre tes fameuses dérivées partielles, ben il suffit de développer les
P.S. en plus, vu qu'il te le faut qu'à l'ordre 6 (i.e. uniquement les termes en
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Salut,
Bon, déjà (et comme d'hab...) il a falu que je cherche quoi c'était le développement de "Mac Laurin" (tout ce qui est nom propres, il n'y a rien qui rentre...) et en fait, c'est le développement limité en 0 (donc ici en (0,0)) ce qui facilite en général grandement les choses...
Ensuite, pour des fonctions de plusieurs variables, le "petit o" de la fin du D.L., c'est un "petit o" en la norme du (petit) vecteur X ce qui fait qu'ici, c'est "fingers in the noze" vu que la fonction ne dépend que de la norme du vecteur (x,y).
Conclusion : le truc que tu cherche, c'est (on ne peut plus bètement) :
Et, à la limite, si tu veut absolument voir apparaitre tes fameuses dérivées partielles, ben il suffit de développer les
P.S. en plus, vu qu'il te le faut qu'à l'ordre 6 (i.e. uniquement les termes enavec
, il suffit de prendre les 2 premiers termes du D.L. de
.
Je n'y avais pas pensé
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
