Systèmes d'équations à n inconnus

[Lilou123]

Bonjour,

Je ne comprends pas comment résoudre un système à 3 équations et 4 inconnus ainsi qu'un système à 5 équations et 3 inconnus, si quelqu'un pouvez m'aider ça serait gentil..





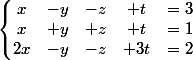
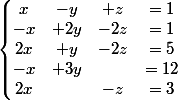
Merci d'avance

Lilou

[siger]

Bonjour

il y a plusieurs methodes, mais .......
dans un systeme lineaire de n equations independantes a m inconnues :
si m>n on peut calculer n inconnues en fonction des m-n restantes
si m=n on peut calculer n inconnues
si m<n en general le systeme n'a pas de solution

Dans le premier exercice on peut poser k = y + z ..
ce qui ramene a 3 inconnues et obtenir x,t, k ( donc y dependra de z ou l'inverse)
dans le second cas il ne devrait pas y avoir de solutions (si les equations sont independantes....
ce qui ne semble pas etre le cas a posteriori, compte tenu des deux dernieres equations qui ramenent a un systeme de 3 equations a 3 inconnues, x=z=3, y=5)

[pascal16]

Vue géométriquement :

Pour le second système :
tu cherches si 5 plans ont au moins 1 point en commun.
Le classique 3*3, si les plans ne sont pas parallèles 2 à 2, te donne l'unique point contenu dans les 3 plans. Deux équations supplémentaires, c'est vérifier si deux autres plans passent aussi par ce point.

Pour un système 2 équations, 3 inconnues.
cette fois tu cherches l'intersection de 2 plans dans l'espace.
cas général -> c'est une droite (écrite de façon paramétrique, tu as 1 seule dimension)
cas particuliers : les deux plans sont strictement parallèles (pas de sol) ou confondus (le plan entier est solution)

[chan79]

salut
Dans le premier cas, on peut montrer assez vite qu'il est nécessaire que t=-3 et x=5
Pour le second, on résout d'abord avec les trois premières égalités.

[pascal16]

pour la seconde :
2 fois (1) + (2) donne x=3
injecté dans (4) donne y=5 et injecté dans (5) donne z=3
les équations (4) et (5) sont alors vérifiée. Reste à vérifier si (3;5;3) est solution de (1);(2) et (3), ce qui est vrai.
D'un point de vu théorie vectorielle, les équations sont liées.
(3;5;3) est donc l'unique solution (les 5 plans se coupent bien en 1 point unique)

[pascal16]

pour la (1).
Une méthode peut être la méthode du pivot de Gauss
SI les équations ne sont pas liés, tu te trouves avec az + bt=c
tu poses z=f(t)
en remontant, tu as y=g(z,t) donc y=h(t)
en remontant , ...... x= i(t)
c'est une équation paramétrique. Tu as au moins 4 choix de paramètres. Donc les solution peuvent paraître différentes alors qu'elles sont identiques. Ici, il me semble qu'on tombe sur des pivots nuls et qu'il faut échanger des lignes pour finir proprement. Mais c'est un travail par équivalence.

On voit des lignes quasi identiques, on peut commencer par des implications.
(1)-(3) te donne -x-2t=1
(1)+(2) te donne x+t=2
donc t=-3 et x =5
(pour épater la galerie 2*(1)+(2)-(3) donne directement t)
Mais ce n'est qu'une implication, on remplace ensuite dans le système du départ les valeurs trouvées.
il reste 3 équations qui sont en fait identiques y+z=-1.
Une écriture de la solution est x=5, t=-3 et y+z=-1.
En physique, LA seule solution est, à l'instant t=-3, dans le plan d'équation x=-3, la droite y+z=-1