Systeme de 3 equations à 3 inconnus
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
algebriquus
- Messages: 4
- Enregistré le: 27 Fév 2015, 11:43
-
 par algebriquus » 27 Fév 2015, 11:52
par algebriquus » 27 Fév 2015, 11:52
Bonjour, je suis amener a résoudre un système de trois équations à trois inconnus j'ai beau me creuser la tête pas moyen de mettre la main sur des équations en fonction de A,B,C
x=cos(A)[V*cos(B)+W*cos(B+C)]
y=U+V*sin(B)+W*sin(B+C)
z=-sin(A)*[V*cos(B)+W*cos(B+C)]
ou U = 0.175; V=0.16; W=0.16;
j'ai réussi à trouver A = arctan(-z/x) mais je n'arrive pas a trouver les autres...
Je poste donc pour savoir si vous avez une idée de la démarche que je peux utiliser pour résoudre ces équations. Merci d'avance.
-
mathelot
 par mathelot » 27 Fév 2015, 13:22
par mathelot » 27 Fév 2015, 13:22
si je comprend bien
x,y,z sont des paramètres , U ,V,W des constantes et A,B,C les inconnues,
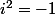
}+i(y-U)=e^{iB} \left( V +We^{iC} \right))
en passant au carrés des modules
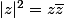
}+(y-U)^2= V^2+W^2+2VWcos(C))
d'où le calcul de cos(C)
-
mathelot
 par mathelot » 27 Fév 2015, 13:27
par mathelot » 27 Fév 2015, 13:27
-
mathelot
 par mathelot » 27 Fév 2015, 13:38
par mathelot » 27 Fév 2015, 13:38
algebriquus a écrit:y=U+V*sin(B)+W*sin(B+C)
z=-sin(A)*[V*cos(B)+W*cos(B+C)]
.
}+i(y-U)=e^{iB} (V+We^{iC}))
}+i(y-U)=e^{iB} \left( V +We^{iC} \right))
-
algebriquus
- Messages: 4
- Enregistré le: 27 Fév 2015, 11:43
-
 par algebriquus » 27 Fév 2015, 14:05
par algebriquus » 27 Fév 2015, 14:05
mathelot a écrit:}+i(y-U)=e^{iB} (V+We^{iC}))
}+i(y-U)=e^{iB} \left( V +We^{iC} \right))
en fait je recherche A B et C (j'ai déjà A en fonction de x et z)
l'objectif serait d'isolé B et C de la même façon.
Pour A j'ai trouver pareil en divisant x par z
ÉDIT: Merci pour le C je viens de comprendre votre calcul c'est bien pensé d'utiliser la tangente pour retrouver le COS.
-
mathelot
 par mathelot » 27 Fév 2015, 14:31
par mathelot » 27 Fév 2015, 14:31
algebriquus a écrit:x=cos(A)[V*cos(B)+W*cos(B+C)]
y=U+V*sin(B)+W*sin(B+C).
on quotiente
cos(A)}{x}=\frac{V*sin(B)+W*(sin(B)cos(C)+cos(B)sin(C))}{V cos(B)+W(cos(B)cos(C)-sin(B)sin(C))})
cos(A)}{x}=\frac{(V+Wcos(C))*tan(B)+W*sin(C))}{V +W(cos(C)-tan(B)sin(C))})
la formule est homographique, permet d'obtenir tan(B) en fonction de C
=\frac{x*W*sin(C)-(y-U)cos(A)(V+Wcos(C))}{-(y-U)cos(A)Wsin(C)-x(V+Wcos(C))})
=\frac{-x*W*sin(C)+(y-U)cos(A)(V+Wcos(C))}{(y-U)cos(A)Wsin(C)+x(V+Wcos(C))})
-
algebriquus
- Messages: 4
- Enregistré le: 27 Fév 2015, 11:43
-
 par algebriquus » 27 Fév 2015, 14:48
par algebriquus » 27 Fév 2015, 14:48
cela doit fonctionner aussi par substitution non?
-
mathelot
 par mathelot » 27 Fév 2015, 14:55
par mathelot » 27 Fév 2015, 14:55
oui......................
-
algebriquus
- Messages: 4
- Enregistré le: 27 Fév 2015, 11:43
-
 par algebriquus » 27 Fév 2015, 15:19
par algebriquus » 27 Fév 2015, 15:19
mathelot a écrit:oui......................
Ok ;D jvais essayer de substituer ;D En tout cas merci beaucoup! :lol3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
