Bonjour
Je voudrais vous demander si on peut doter N, l'ensemble des entiers naturels d'une structure de corps. Si oui laquelle, si non comment on peut le démontrer.
Merci d'avance
Sur la structure de N
6 messages
- Page 1 sur 1
par Ben314 » 10 Déc 2009, 15:33
Si tu accepte "d'inventer" une addition et une multiplication, alors la réponse est (évidement) oui car, comme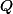 
est dénombraple, il existe une bijection 
de 
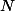dans 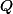et il est clair que, si on pose (par définition) pour 
:
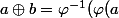+\varphi(b)))
et \times\varphi(b)))
alors,)
est un corps !!!!
Par contre (tout aussi évidement), cela ne marche pas si on veut garder l'addition et/ou la multiplication "usuelle" sur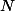
alors,
Par contre (tout aussi évidement), cela ne marche pas si on veut garder l'addition et/ou la multiplication "usuelle" sur
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par euler21 » 10 Déc 2009, 16:03
donc si deux ensembles sont équipotents, alors ils peuvent avoir la même structure algébrique ??
par Ben314 » 10 Déc 2009, 16:10
Evidement que oui !!!!
A condition de laisser complètement tomber les éventuelles structures qu'il avaient l'un et l'autre.
Si tu veux, pour "parler simple", tu prend un isomorphisme et tu "enlève" les structures, il reste.... une bijection...
par exemple les opérations dont je munie N dans l'exemple ci-dessus n'on absolument rien à voir avec l'addition et la multiplication usuelles sur N.
P.S. En général, ce genre de constructions n'a absolument aucun intérêt en math. car on considère (presque) toujours les ensembles avec leurs structures.
A condition de laisser complètement tomber les éventuelles structures qu'il avaient l'un et l'autre.
Si tu veux, pour "parler simple", tu prend un isomorphisme et tu "enlève" les structures, il reste.... une bijection...
par exemple les opérations dont je munie N dans l'exemple ci-dessus n'on absolument rien à voir avec l'addition et la multiplication usuelles sur N.
P.S. En général, ce genre de constructions n'a absolument aucun intérêt en math. car on considère (presque) toujours les ensembles avec leurs structures.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par willouuu » 14 Déc 2009, 07:03
J avais lu ce post en passant sur le forum ce week end et j'avou qu'il me posait problème. En effet tu as bien défini des lois internes mais rien n'assure qu'elles soit associative par exemple.
Ta méthode suggère un transfert de structure via isomorphisme. Je ne suis pas tout à fait sûr que cela soit possible dans le cas présent. En tout cas je vais voir ce que je peux trouver là-dessus.
Ta méthode suggère un transfert de structure via isomorphisme. Je ne suis pas tout à fait sûr que cela soit possible dans le cas présent. En tout cas je vais voir ce que je peux trouver là-dessus.
par Skullkid » 14 Déc 2009, 13:09
Les lois données par Ben sont associatives :
= f^{-1}(f(a)+f(b\oplus c))= f^{-1}(f(a)+f(b)+f(c))=f^{-1}(f(a \oplus b)+f(c))= (a \oplus b) \oplus c)
Et je pense pouvoir affirmer sans grande crainte qu'elles vérifient tous les axiomes de corps. En fait ça revient juste à numéroter les rationnels, et au lieu de dire que 1 + 1/2 = 3/2 on dit que le numéro 2 + le numéro 15 = le numéro 37. Bref, on renomme les éléments de
.
Après en effet ça n'a pas l'air très utile ^^
Et je pense pouvoir affirmer sans grande crainte qu'elles vérifient tous les axiomes de corps. En fait ça revient juste à numéroter les rationnels, et au lieu de dire que 1 + 1/2 = 3/2 on dit que le numéro 2 + le numéro 15 = le numéro 37. Bref, on renomme les éléments de
Après en effet ça n'a pas l'air très utile ^^
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :