Sur la notation de Landau "petit o"
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 12 Mar 2018, 12:59
par Ben314 » 12 Mar 2018, 12:59
chombier a écrit:Mon explication à moi :
1) Techniquement
)
et
)
sont des ensemble, et on devrait donc écrire
) (f' + o(g')))
. . .
Non, même en considérant que c'est des ensembles, tu va quand même "te faire voler" vu que tu trouvera partout dans les cours/bouquins/poly./solutions d'exo des trucs du style :
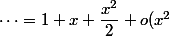\ {\red=}\ 1+x+o(x))
Où le

en terme d'ensemble, c'est une inclusion et pas une égalité ce qui signifie que réciproquement, ça :
\ {\red=}\ 1+x+\dfrac{x^2}{2}+o(x^2))
tu le trouvera écrit nulle part et je pense que n'importe quel correcteur va considérer que c'est faux...
Bref, à mon avis, il n'y a pas moyen de dire autre chose que le fait qu'avec ces notations de Landau, la relation d'égalité perd son statut symétrique (mais reste réflexive et transitive).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 12 Mar 2018, 13:32
par Pseuda » 12 Mar 2018, 13:32
chombier a écrit:Peut-être que toi non plus tu n'as pas encore compris ce qu'est un petit o()

Ou c'est peut-être @aviateur


-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 12 Mar 2018, 13:34
par chombier » 12 Mar 2018, 13:34
Oui bien sûr dans ma tête je remplace aussi les égalités par des inclusions :
 \subset o(x))
mais l’inclusion réciproque est fausse.
Cela permet d’utiliser le signe égal quand il y a double
Inclusion :
 + o(x) \subset o(x))
et
 \subset o(x) + o(x))
donc :
 + o(x) = o(x))
, et c’est une vraie égalité d’ensembles.
Cela permet de différentier les "=" avec perte d’information (les inclusions déguisées) des "=" sans perte d’information.
Bref je ne changerais pas la monde, mais je peux changer ma façon de voir le monde

-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 12 Mar 2018, 13:40
par Pseuda » 12 Mar 2018, 13:40
Il n'y a pas de vol à mon sens non plus, car tout dépend de ce qu'on veut en faire (par exemple pour calculer une limite). Puisque l'analogie avec l'écriture décimale a bien marché, par exemple si on veut calculer l'aire d'un cercle à une précision 10^(-2) cm^2 et que son rayon = 1/3 cm, une approximation de pi à 3,14 est suffisante.
Il y aurait vol si on s'était décarcassé à obtenir une précision de pi avec 20 chiffres après la virgule, pour obtenir l'aire de ce cercle à une précision 10^(-2) !
Modifié en dernier par
Pseuda le 12 Mar 2018, 13:59, modifié 1 fois.

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 12 Mar 2018, 13:57
par chombier » 12 Mar 2018, 13:57
Ben314 a écrit:Bref, à mon avis, il n'y a pas moyen de dire autre chose que le fait qu'avec ces notations de Landau, la relation d'égalité perd son statut symétrique (mais reste réflexive et transitive).
Et comme on a l´antisymetrie ça fait de cette egalite une relation d’ordre. Ce qui est somme toute logique puisque cette égalité est in fine une inclusion déguisée
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
et
sont des ensemble, et on devrait donc écrire
. . .
