Notation de landau

par **legeniedesalpages** » 01 Oct 2007, 22:50

Bonsoir,

je ne vois pas comment montrer que

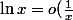si

.

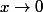
Il faut donc montrer que pour tout

, il existe

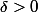
tel que
[CENTER]

[/CENTER]

Mais je n'arrive pas à saisir une piste. Merci pour votre aide.

par **Nightmare** » 01 Oct 2007, 23:04

Salut :happy3:

Donc

avec

d'où

:happy3:

par **legeniedesalpages** » 01 Oct 2007, 23:12

Salut Nightmare,

en fait je comptais voir pourquoi

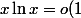juste après et voir pourquoi cela signifie que

si

.

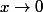
Et dans démonstration pourquoi tu n'envisages pas le cas où

?

Edit: ah oui pardon elles ne sont pas définies en 0.

par **Nightmare** » 01 Oct 2007, 23:15

Ben je ne pense pas qu'on puisse justifier que xln(x) tend vers 0 en 0 en utilisant le résultat ln(x)=o(1/x).

En tout cas, je vois mal comment on va se débrouiller pour trouver le epsilon que tu demandes.

Selon moi, et je viens de vérifier dans mon livre de maths, ln(x)=o(1/x) découle bien du fait que xln(x) tend vers 0 en 0.

Je vais me coucher, bonne nuit.

:happy3:

par **legeniedesalpages** » 01 Oct 2007, 23:17

oki d'accord, je m'y prends pas dans le bon sens.
Merci pour ton aide en tout cas, bonne nuit :dodo:

Notation de landau

notation de landau

Qui est en ligne