Sup d'une fonction

[Robot]

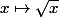
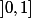
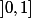
C'est juste que est une bijection de sur . Ca explique tout, inutile d'aller chercher plus loin.

[Lostounet]

Je crois que ce changement de variable bijectif conserve la fonction toute entière pas juste son sup.

Pour tout x dans ]0; 1] il existe un unique t de ]0; 1] tel que t = Vx
Cela rend l'expression f(Vx)/x^(1/4) égale à f(t)/Vt sur l'intervalle choisi.

A confirmer par Robot

[Robot]

Si est n'importe quelle application surjective de l'ensemble sur l'ensemble et si est une fonction de dans majorée par une constante, alors l'image de par est égale à l'image de par et donc

[FLY TS]

SALUT

:cry: aider moi à résoudre cette équation à deux inconnu :

N=PxQ, Q et P sont des inconnu.
trouver Q et P. :cry:

[FLY TS]

aider moi please :cry: :cry: :cry:

[Lostounet]

SALUT

aider moi à résoudre cette équation à deux inconnu :

N=PxQ, Q et P sont des inconnu.
trouver Q et P.

Merci de créer ta propre discussion dans la section Lycée

[Robot]

Si la fonction n'est pas majorée sur , tu auras du mal à prendre son sup sur , tout simplement !
Par définition, est la borne supérieure de l'image de par . Pourquoi donc te compliques-tu la vie ?

[Robot]

Oui, la preuve est correcte. Mais inutile, puisqu'on prend la borne supérieure de deux sous-ensembles égaux de , et tu as justement remarqué que ces deux sous-ensembles sont égaux. Le point essentiel de la preuve que tu as écrite est une re-démonstration de l'égalité des deux sous-ensembles.