Etude fonction - Sup TSI
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
LeGioon
- Messages: 9
- Enregistré le: 17 Avr 2014, 20:00
-
 par LeGioon » 22 Juin 2014, 21:29
par LeGioon » 22 Juin 2014, 21:29
Bonjours,
je viens demander votre aide car je n'arrive pas a démarrer un exercice, voici l'énoncer :
" On pose f
n(x) =

; montrer que fn(x) = 0 admet une unique solution an dans IR+ et calculer la limite de (an) "
Voilà je ne sais pas par ou commencer et comment m'y prendre et quelle outils utiliser, donc si vous pouviez me donner un peut d'aide !
Dans l'attente d'une réponse, cordialement.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 22 Juin 2014, 21:36
par zygomatique » 22 Juin 2014, 21:36
salut
théorème des valeurs intermédiaires ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 22 Juin 2014, 21:43
par zygomatique » 22 Juin 2014, 21:43
f(0) = -1
ensuite
 = - \dfrac {1 - (-x)^{n+1}}{1 + x})
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
LeGioon
- Messages: 9
- Enregistré le: 17 Avr 2014, 20:00
-
 par LeGioon » 22 Juin 2014, 22:00
par LeGioon » 22 Juin 2014, 22:00
Merci, je vais essayer !

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 22 Juin 2014, 22:01
par Ben314 » 22 Juin 2014, 22:01
LeGioon a écrit:..." On pose f
n(x) =

Pas clair du tout ton truc : c'est quoi qu'il y a dans les points de suspension ?
- Soit c'est une alternance de + et -, et ça devrait se terminer par
^{n-1}x+(-1)^n\)
ou alors il faudrait que l'énoncé précise qu'on ne considère que des

impairs.
- Soit c'est que des + et ça aurait pas été con d'en mettre un ou deux de plus pour que se soit compréhensible...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 23 Juin 2014, 20:03
par deltab » 23 Juin 2014, 20:03
Bonsoir,
zygomatique a écrit:f(0) = -1
ensuite
 = - \dfrac {1 - (-x)^{n+1}}{1 + x})
Erreur!
Les seules réelles solutions possibles de
^{n+1})
sont

et

, valeurs exclues.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 23 Juin 2014, 20:04
par deltab » 23 Juin 2014, 20:04
Bonsoir,
zygomatique a écrit:f(0) = -1
ensuite
 = - \dfrac {1 - (-x)^{n+1}}{1 + x})
Erreur!
Les seules solutions réelles possibles de
^{n+1}=0)
sont

et -

, valeurs exclues.
-
LeGioon
- Messages: 9
- Enregistré le: 17 Avr 2014, 20:00
-
 par LeGioon » 23 Juin 2014, 20:17
par LeGioon » 23 Juin 2014, 20:17
Finalement j'ai utilisé le fait que la dérivé de fn(x) est strictement positive sur IR+. Donc fn(x) est strictement continue et croissante sur IR+ donc elle réalise une bijection de IR+ -> [-1;+

] donc elle admet un unique antécédent an tel que fn(an) = 0.
Pour la limite j'ai un peu plus de mal, apparemment il faudrait utiliser un Pn+1(x) puis démontrer que cette suite est décroissante et passer au limite dans cette même équation...
Effectivement Ben314 ce n'est pas très claire mais l'exercice est posé comme cela ...
Cordialement
-
LeGioon
- Messages: 9
- Enregistré le: 17 Avr 2014, 20:00
-
 par LeGioon » 23 Juin 2014, 22:13
par LeGioon » 23 Juin 2014, 22:13
Excusez moi il y a comme une erreur de signe dans l'énoncer je viens de m'en rendre compte ...
C'est f
n(x) =


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Juin 2014, 23:59
par Ben314 » 23 Juin 2014, 23:59
LeGioon a écrit:Excusez moi il y a comme une erreur de signe dans l'énoncer je viens de m'en rendre compte ...
C'est f
n(x) =

Là, les points de suspensions sont nettement plus compréhensible et l'énoncé est nettement plus interessant vu qu'on ne sait pas résoudre l'équation de façon exacte.
Concernant la solution, ce n'est pas compliqué :
1) Il est clair que f'>0 sur ]0,+oo[ et, comme f(0)=-11/2 fixé, la limite de f_n(a) lorsque n->oo : tu en déduit un encadrement de a_n qui te donne la limite.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
LeGioon
- Messages: 9
- Enregistré le: 17 Avr 2014, 20:00
-
 par LeGioon » 24 Juin 2014, 09:20
par LeGioon » 24 Juin 2014, 09:20
C'est à dire evaluer f_n(1/2) ? Trouver a quoi c'est égale ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 24 Juin 2014, 09:58
par Ben314 » 24 Juin 2014, 09:58
LeGioon a écrit:C'est à dire evaluer f_n(1/2) ? Trouver a quoi c'est égale ?
Oui, le calculer, si tu préfère.
Ici, le but c'est surtout de trouver son signe : vu que les fonction f_n sont croissante tou a tel que fn(a)0 te donne un majorant.
Il y aurait pas mal d'autre méthodes pour trouver la limites des an, par exemple de commencer par montrer qu'elle est décroissante (saurait tu le faire ?) ce qui assurerais que la limite existe.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Black Jack
 par Black Jack » 24 Juin 2014, 09:58
par Black Jack » 24 Juin 2014, 09:58
2)
x^n + x^(n-1) + ... + x est la somme de n termes en progression géométrique de raison x et de 1er terme = x --->
x^n + x^(n-1) + ... + x = x.(x^n - 1)/(x - 1) (avec x différent de 1)
L'équation devient donc :
x.(x^n - 1)/(x - 1) = 1 (avec x >= 0 et différent de 1)
x.(x^n - 1) = (x-1)
x^(n+1) - 2x + 1 = 0
Pour n --> +oo, il ne peut pas y avoir de solutions réelles > 1 car alors x^(n+1) > > 2x et donc x^(n+1) - 2x + 1 > 0
Donc la solution (qui existe comme montré dans la partie 1 de l'exercice) est forcément pour 0 < x < 1 et alors x^(n+1) < < 2x pour n --> +oo
Pour n --> +oo, l'équation est pratiquement équivalente à -2x + 1 = 0
et donc la solution tend vers 1/2 pour n --> +oo
*****
Il y a probablement une approche plus jolie, mais soit.
:zen:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 24 Juin 2014, 10:03
par Ben314 » 24 Juin 2014, 10:03
A mon avis, le problème, c'est le "...l'équation est pratiquement équivalente à..." : sur une copie d'exam, ça passe pas ça...
Mais en utilisant par exemple la monotonie de la fonction x^(n+1) - 2x + 1, tu peut remplacer ton "pratiquement équivalente" par un encadrement : ça fait plus sérieux... :zen:
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 24 Juin 2014, 16:12
par deltab » 24 Juin 2014, 16:12
Bonjour,
Ben314 a écrit:A mon avis, le problème, c'est le "...l'équation est pratiquement équivalente à..." : sur une copie d'exam, ça passe pas ça...
Mais en utilisant par exemple la monotonie de la fonction x^(n+1) - 2x + 1, tu peut remplacer ton "pratiquement équivalente" par un encadrement : ça fait plus sérieux... :zen:
On peut montrer que la suite de fonctions
)
converge uniformément sur

vers
= \dfrac{x}{1-x}-1)
. On aura alors :
=f(u))
. La suite

donnée est positive décroissante, alors
=0=f(a))
où
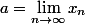
.

est donc solution de
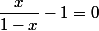
ce qui donne
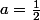

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 24 Juin 2014, 19:47
par Ben314 » 24 Juin 2014, 19:47
ça effectivement, c'est nettement plus sérieux,
mais je suis prêt à parier deux cacahuètes contre un camembert que LeGioon n'a pas encore vu la notion de convergence uniforme.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 25 Juin 2014, 10:49
par zygomatique » 25 Juin 2014, 10:49
pour revenir à la réponse de Black Jack :: ta démonstration est correcte si tu rédiges correctement ::
les racines appartiennent à l'intervalle [0, 1[ et vérifient :: [quote]x_n^n = 2x_n + 1[TEX]
en faisant tendre n vers l'infini alors les deux membres tendent vers 0 (puisqu'ils sont égaux et que le premier tend vers 0) donc x(n) tend vers 1/2 ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 25 Juin 2014, 16:34
par deltab » 25 Juin 2014, 16:34
Bonjour
zygomatique a écrit:pour revenir à la réponse de Black Jack :: ta démonstration est correcte si tu rédiges correctement ::
les racines appartiennent à l'intervalle [0, 1[ et vérifient ::
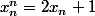
en faisant tendre n vers l'infini alors les deux membres tendent vers 0 (puisqu'ils sont égaux et que le premier tend vers 0) donc x(n) tend vers 1/2 ....
Erreur de frappe:
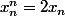


Attention, l'implication
^n \to 0)
est erronée comme le prouve
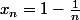
, il fallait y ajouter
^n \to a, 0 \le a<1)

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 25 Juin 2014, 19:00
par zygomatique » 25 Juin 2014, 19:00
deltab a écrit:Bonjour
Erreur de frappe:
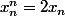


Attention, l'implication
^n \to 0)
est erronée comme le prouve
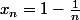
, il fallait y ajouter
^n \to a, 0 \le a<1)
effectivement ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 25 Juin 2014, 19:27
par Ben314 » 25 Juin 2014, 19:27
zygomatique a écrit:les racines appartiennent à l'intervalle [0, 1[ et vérifient :
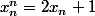
en faisant tendre n vers l'infini alors les deux membres tendent vers 0 (puisqu'ils sont égaux
et que le premier tend vers 0) donc x(n) tend vers 1/2 ....
ça fonctionne à condition d'avoir montré que, non seulement x_n est dans [0,1[, mais qu'il est (à partir d'un certain rang) dans un certain [0,b[ avec b0 fixé) et en déduire sans le moindre argument supplémentaire (avec la définition même d'une limite ) que xn tend vers 1/2.
Juste pour évaluer la longueur de la preuve, en rédigeant absolument tout bien comme il faut, ça donnerais :
a) La fonction

est dérivable sur
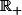
et, pour tout
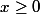
,
=nx^{n-1} + (n-1)x^{n-2} + ... + x +1>0)
donc

est strictement croissante sur
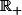
.
Or
=-10)
donc il existe
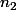
tel que, pour tout

=0<f_n(\frac{1}{2}+\varepsilon))
et donc

(car

est strictement croissante)
Les deux points ça dessus montrent (par définition d'une limite) que
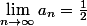
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 84 invités
