bonjour, j'ai euce ujet en examen terminal de licence et étant au rattrapage et qu'il y aura lemem type d'exercice j'aurais aimé que quelqu'un m'aide a le realiser car le rattrapage est lundiet je ne comprend pas. aidez moi svppp !!!!!!
je vous remercie d'avance.
Une personne emprunte une somme S, le 1er janvier 2008, à un taux d'interêt annuel t. Elle remboursera par annuités constantes notées A et versées chaque 1er janvier, pendant p années, à partir du 1er janvier 2009. On note Cn le capital restant dû le 1er janvier de l'année 2008+n (après le calcul des intérêts et le versement de la nième annuité A), n étant une entier inférieur ou égal à p.
1)a) Calculer C1 et C2. établir une relation entre Cn et Cn+1. Préciser la nature de la suite {Cn}.
Démontrer que Cn=(1+t)^n [S- (A/t)] + (A/t)
Indiquez la valeur numérique de Cp.Montrer que:
t
A= S -------------
1-(1+t)^-p
En déduire que
(1+t)^p -(1+t)^n
Cn= S[ -------------------]
(1+t)^p - 1
b) on note I le montant total des interets versés en p années.
exprimer I en fonction de S de p et de A.
montrer que I/S = tp
----------- --- -1
1 - (1+t)^-P
Sujet exam suites maths financières
3 messages
- Page 1 sur 1
C'est pas tellement des maths ton truc, mais je pense qu'on peut quand même t'aider...
 est le capital restant dû (CRD) le 1er janvier 2009.
est le capital restant dû (CRD) le 1er janvier 2009.
D'abord tu dois te demander combien il aura remboursé de capital lors de sa première annuité, qui est d'ailleurs le même jour (dans ces cas là on considère toujours que l'annuité est déjà versée, i.e. on parle du CRD le 1er janvier 2009 au soir). Tu dois donc calculer . Or tu connais la formule :
. Or tu connais la formule :
^2}+...+\frac{A}{(1+t)^p}=A\frac{1-(1+t)^{-p}}{t})
Maintenant que tu as isolé ton , tu vas pouvoir calculer
, tu vas pouvoir calculer  et
et  . Tu sais qu'à chaque échéance, l'emprunteur rembourse des intérêts et du capital.
. Tu sais qu'à chaque échéance, l'emprunteur rembourse des intérêts et du capital.
Combien rembourse-t-il d'intérêts ?
Tout simplement fois le CRD en début de période, soit pour la première échéance (ou annuité) :
fois le CRD en début de période, soit pour la première échéance (ou annuité) : 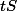 .
.
Le reste de la somme remboursée, c'est-à-dire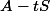 sera donc l'amortissement (remboursement du capital pour cette période).
sera donc l'amortissement (remboursement du capital pour cette période).
Le capital restant dû le premier janvier 2009 sera donc :) (n'oublie pas qu'on a trouvé une expression de
(n'oublie pas qu'on a trouvé une expression de  plus haut)
plus haut)
Pour la deuxième, ça sera dans le même genre. Je te laisse y réfléchir.
Pour la récurrence, tu devrais y arriver en arrangeant bien les résultats trouvés pour et
et  .
.
Pour le reste de l'exercice, désolé mais je ne comprends rien à ce que tu as mis. Je ne pourrai de toute façon pas t'aider plus avant lundi. Alors bonne chance !
D'abord tu dois te demander combien il aura remboursé de capital lors de sa première annuité, qui est d'ailleurs le même jour (dans ces cas là on considère toujours que l'annuité est déjà versée, i.e. on parle du CRD le 1er janvier 2009 au soir). Tu dois donc calculer
Maintenant que tu as isolé ton
Combien rembourse-t-il d'intérêts ?
Tout simplement
Le reste de la somme remboursée, c'est-à-dire
Le capital restant dû le premier janvier 2009 sera donc :
Pour la deuxième, ça sera dans le même genre. Je te laisse y réfléchir.
Pour la récurrence, tu devrais y arriver en arrangeant bien les résultats trouvés pour
Pour le reste de l'exercice, désolé mais je ne comprends rien à ce que tu as mis. Je ne pourrai de toute façon pas t'aider plus avant lundi. Alors bonne chance !
Bj,
il s'agit d'un échéancier de remboursement classique:
hint:
Il faut comprendre, dans une dette, il n'y a que le capital qui est dû.
Les intérêts sont là pour tenir compte du différé de remboursement.
L'échéancier se termine donc quand tout le capital a été remboursé
(on dit: son "intégralité")
A la 1ère échéance, on paye A:
Dans A, il y a une part d'intérêt ,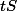
et le reste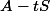 est un remboursement de capital.
est un remboursement de capital.
Le capital dû passe donc de
S à S-(A-tS)=(1+t)S-A
Cette formule est valable chaque année et conduit
à une définition par récurrence du capital restant dû
C_{n-1}-A) (**)
(**)
Ce type de suite , de terme général) s'appelle
s'appelle
arithmético-géométrique.
étude du point fixe de la suite arithméético-géométrique
si la suite) a une limite
a une limite  , alors
, alors  vérifie l'équation:
vérifie l'équation:
C_{n-1}-A \\<br />\lambda=(1+t)\lambda-A \\)
en soustrayant membre à membre,on voit que la nouvelle
suite de terme général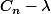 est géométrique de raison (1+t).
est géométrique de raison (1+t).
D'autre part ,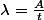
d'où
 (1+t)^n)
car il s'agit d'une suite géométrique de raison q=1+t et de 1er terme
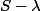
En remplaçant par sa valeur,on obtient la formule désirée.
par sa valeur,on obtient la formule désirée.
il s'agit d'un échéancier de remboursement classique:
hint:
Il faut comprendre, dans une dette, il n'y a que le capital qui est dû.
Les intérêts sont là pour tenir compte du différé de remboursement.
L'échéancier se termine donc quand tout le capital a été remboursé
(on dit: son "intégralité")
A la 1ère échéance, on paye A:
Dans A, il y a une part d'intérêt ,
et le reste
Le capital dû passe donc de
S à S-(A-tS)=(1+t)S-A
Cette formule est valable chaque année et conduit
à une définition par récurrence du capital restant dû
Ce type de suite , de terme général
arithmético-géométrique.
étude du point fixe de la suite arithméético-géométrique
si la suite
en soustrayant membre à membre,on voit que la nouvelle
suite de terme général
D'autre part ,
d'où
car il s'agit d'une suite géométrique de raison q=1+t et de 1er terme
En remplaçant
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
