Bonjour ,
Je travaille sur un exercice sur les suites. L' énoncé donne la suite Un définie par Un = ln ( Un-1 + 3).
n-1 et n étant des indices.
Je n' arrive pas à démontrer la croissance de la suite ni le fait qu elle soit convergente , meme si j' arrive à le conjecturer grace à une représenbtation graphique.
Je serais trés reconnaissante de votre aide
Suites croissance
12 messages
- Page 1 sur 1
le premier terme est Uo= 0 puis on doit également le faire en prenant Uo = 5
J ai essayé de voir le signe de Un+1- Un ou de voir si le quotient est inférieur ou supérieur à 1 sans réel succès.
Autrement avec un raisonnement par récurrence je m embrouille les pinceaux.
Je ne sais pas quoi supposer , on a bien U1 > Uo mais aprés je ne sais pas quoi faire , il me semble bizarre de supposer Un+1 > Un. bref je ne sais pas quelle méthode faire.
J ai également essayé d' étudier le signe de la fonction Un+1 - Un mais elle est positive puis négative et je n' aarive pas à trouver la valuer d' annulation.
J ai essayé de voir le signe de Un+1- Un ou de voir si le quotient est inférieur ou supérieur à 1 sans réel succès.
Autrement avec un raisonnement par récurrence je m embrouille les pinceaux.
Je ne sais pas quoi supposer , on a bien U1 > Uo mais aprés je ne sais pas quoi faire , il me semble bizarre de supposer Un+1 > Un. bref je ne sais pas quelle méthode faire.
J ai également essayé d' étudier le signe de la fonction Un+1 - Un mais elle est positive puis négative et je n' aarive pas à trouver la valuer d' annulation.
Essaye de te repérer par rapport au point fixe de f. Ici, on a un point fixe entre 0 et 5. Si ton premier terme est en dessous de ce point fixe t. Alors 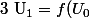\le f(t)=t) (l'inégalité est vraie car f est croissante)
(l'inégalité est vraie car f est croissante)
de même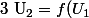\le f(t)=t) etc. On déduit facilement par récurrence que
etc. On déduit facilement par récurrence que  .
.
Essaye de voir ce que tu peux faire lorsque le premier terme est supérieur au point fixe.
de même
Essaye de voir ce que tu peux faire lorsque le premier terme est supérieur au point fixe.
Tu n'as pas vraiment besoin de déterminer la[les] valeur[s] exactes des éventuels points fixes : le tout est de montrer qu'il y en a un (ou plusieurs) et de savoir où il[s] se situe[nt] par rapport à to Uo.clemenceB a écrit:Mais sans ce servir d un graphique comment est ce qu on peut determiner le point fixe ?
Es essayant?
Pour montrr qu'un réel tel que... existe il suffit souvent d'étudier une fonction bien choisie et de montrer à l'aide du tableau de variation qu'elle s'annule...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
