Suites et continuité uniforme d'une application

[Guigui1Pierre]

Bonjour,
Je reste bloqué sur cette démo:

E et F deux ev normés
f une application de E dans F

[ Pour toutes suites u et v d'éléments de E: lim(u-v)=0 => lim(f(u(n))-f(v(n)))=0 ]
implique: f uniformément continue

Soit epsilon>0
Il me suffirait de trouver un delta>0 tel que pour tout (x,y) de E² N(x-y)<delta => N((f(x)-f(y))<epsilon

PS: j'ai bien remarqué l'éditeur d'équation en haut à droite mais je n'arrive pas à m'en servir...

Merci d'avance,

Guillaume

[tournesol]

Je n'ai pas le temps de t'aider mais une démo par l'absurde devrait convenir .

[GaBuZoMeu]

Si n'est pas uniformément continue, il existe tel que pour tout entier naturel il existe et dans 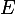tels que et ...

[Guigui1Pierre]

D'accord. Merci.
J'avais pensé à la suite 2 puissance -n. Mais je pensais pas à raisonner par l'absurde.

[tournesol]

Je mesuis trompé : ce n'est pas une démo par l'absurde mais une démo de la contraposée .

[Guigui1Pierre]

euh... Ca veut dire la même chose en gros? (par l'absurde et contraposée)