Etude de la continuité uniforme d'une fonction réelle

[Math3matiqu3]

As-salamu 3ala man itaba3a al-houda,

Bonsoir à tous,

Exo de TD d'Analyse, première année math d'Algérie.

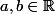(1) Montrer de deux façons différentes que la fonction est uniformément continue sur tout l'intervalle fermé borné de (avec et ).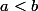

-- Cette fonction est-elle uniformément continue sur ?

(2) La fonction est-elle uniformément continue sur 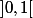? Justifier votre réponse.

J'ai fais la première méthode pour (1) qui consiste à décomposer la fonction en deux fonctions usuelles uniformément continues sur [a,b] ( à savoir et )

Pour la deuxième méthode, (sûrement avec la définition ) Je ne sais pas trop comment .. De l'aide s'il vous plaît !

[Ben314]

Salut,
Perso, la premère qui me viendrait à l'esprit, c'est juste de dire que la fonction est clairement de classe C1 sur R.
Or toute fonction C1 sur une partie D de R a une dérivée continue donc bornée sur tout segment [a,b] contenu dans D ce qui prouve qu'elle est Lipschitzienne donc uniformément continue sur tout [a,b] contenu dans D.

[Kolis]

Bonjour !
Pour la continuité uniforme sur de penses à utiliser les suites

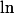
Pour la fonction utilises la suite en notant que l'image d'une suite de Cauchy par une fonction uniformément continue est aussi suite de Cauchy.