Salut !
Connaissez-vous une suite de rationnels dont l'ensemble des valeurs d'adhérence est R tout entier?
Suite de rationnel
6 messages
- Page 1 sur 1
Salut à vous deux !
Bon j'en ai trouvé une non sans mal, et c'est donc avec dépit que je vois votre réponse, si simple...
Pour info, j'avais un truc du genre}{1+v_{3}(n)}) (valuations p-adiques). Si r est rationnel de représentation irréductible p/q, on pose
(valuations p-adiques). Si r est rationnel de représentation irréductible p/q, on pose =2^{p}3^{q-1}p^{n}) avec p premier quelconque différent de 2 et 3. On a clairement
avec p premier quelconque différent de 2 et 3. On a clairement }=r) .
.
Bon j'en ai trouvé une non sans mal, et c'est donc avec dépit que je vois votre réponse, si simple...
Pour info, j'avais un truc du genre
Salut Yos !
Le p présent dans mon extractrice est un autre p, différent de celui dans la fraction p/q mais je pense que tu l'avais compris. Je me suis rendu compte que ça ne marchait pas vraiment pour les relatifs, mais on règle le problème en multipliant x(n) par^{nombre premier}) et en introduit ce facteur premier dans
et en introduit ce facteur premier dans 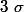 .
.
Le p présent dans mon extractrice est un autre p, différent de celui dans la fraction p/q mais je pense que tu l'avais compris. Je me suis rendu compte que ça ne marchait pas vraiment pour les relatifs, mais on règle le problème en multipliant x(n) par
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

