Suite et racines

par **Aspx** » 12 Mar 2008, 18:15

Bonjour!

Le problème posé est le suivant. Etudier la suite définie par
[CENTER]

[/CENTER]

J'ai montré qu'elle était croissante.
Une idée pour continuer ?

par **yos** » 12 Mar 2008, 18:44

Elle est majorée par 2. J'ai fait ça un peu laborieusement, mais ça marche.

par **xyz1975** » 12 Mar 2008, 18:50

Bonjour,
Calculez

puis montrez que

par **Aspx** » 12 Mar 2008, 18:52

Ca semble assez laborieux comme tu dis ! Puis après avoir montré qu'elle convergeait il faut encore savoir vers quoi... :hein:

par **xyz1975** » 12 Mar 2008, 18:57

Montrer d'abord qu'elle est croissante (je suppose que vous l'avez fait) ensuite il suffit de montrer qu'elle est majorée par 2 (avec l'inégalité que j'ai citée), elle converge vers quoi? ça nous regarde pas.

par **Aspx** » 12 Mar 2008, 19:03

En effet l'exo (posé à l'X) demandait seulement l'étude de la convergence. Merci pour l'idée en tout cas ! (On obtient même avec cette inégalité que la limite est inférieure à

rien de très réjouissant).

par **yos** » 12 Mar 2008, 19:11

J'arrive à

et j'en déduis

donc

à

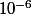
près et du coup

.

par **Aspx** » 12 Mar 2008, 19:11

en effet ! :we:
L'hypothèse de la limite = Phi est plausible vu les valeurs numériques. Simple conjecture ou ?

par **ThSQ** » 12 Mar 2008, 21:05

Aspx a écrit:Une idée pour continuer ?

Il est très facile de montrer que Vn est décroissante (bon, pour n > 2) et que Un < Vn. Conclusion : Un et Vn sont convergentes

par **ThSQ** » 13 Mar 2008, 19:35

Jédusor a écrit:Il est ptetre possible de montrer que U_n est equivalent a
Et on sait que ceci converge vers phi

Douteux vu que u(2) est plus grand que

et que u(n) est croissante.

Suite et racines

Suite et racines

Qui est en ligne