Suite arithmético géometriques
14 messages
- Page 1 sur 1
suite arithmético géometriques
Soit la suite (Un)définie pour tout entier naturel n par (Un+1=4Un-21
U1 = 10)
1. calculer les termes U2, U3 et U4
Soit la suite (Vn) définie pour tout entier naturel n par Vn=Un-7
2.Montrer que la suite (Vn) est une suite géométrique dont on précisera la raison et le premier terme.
3. En deduire l'expression de Vn, en fonction de n
4. En déduir l'expression de Un en fonction de n
Si quelqu'un peut m'aider pour les questions 2,3 et 4 car j'ai pas trop compris
Merci d'avance
U1 = 10)
1. calculer les termes U2, U3 et U4
Soit la suite (Vn) définie pour tout entier naturel n par Vn=Un-7
2.Montrer que la suite (Vn) est une suite géométrique dont on précisera la raison et le premier terme.
3. En deduire l'expression de Vn, en fonction de n
4. En déduir l'expression de Un en fonction de n
Si quelqu'un peut m'aider pour les questions 2,3 et 4 car j'ai pas trop compris
Merci d'avance
B'soir =)
J'ai bien peur que non :/
Ici le but est d'exprimer v_{n+1} en fonction de v_n pour montrer que (v_n) est géométrique et en donner la raison.
On a v_{n+1} = u_{n+1} - 7 <=> v_{n+1} = 4*u_n - 21 - 7 <=> v_{n+1} = ...
Tu devrais arriver sur quelque chose de la forme v_{n+1} = k*v_n, donc avec k la raison de la suite géométrique (v_n).
:)
PS : désolée de m'introduire ici mais le titre était très tentant ;D
J'ai bien peur que non :/
Ici le but est d'exprimer v_{n+1} en fonction de v_n pour montrer que (v_n) est géométrique et en donner la raison.
On a v_{n+1} = u_{n+1} - 7 <=> v_{n+1} = 4*u_n - 21 - 7 <=> v_{n+1} = ...
Tu devrais arriver sur quelque chose de la forme v_{n+1} = k*v_n, donc avec k la raison de la suite géométrique (v_n).
:)
PS : désolée de m'introduire ici mais le titre était très tentant ;D
La chose la plus importante à retenir sur les suites géométriques est que
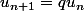 ce qui peux encore se traduire part :
ce qui peux encore se traduire part :
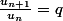
Donc si tu veux montrer qu'une suite est géométrique il faut calculer le quotient de deux termes consécutif, et montrer qu'il est constant ! (et au passage tu as obtenu la raison...)
L'avantage de cette méthode est qu'elle est systématique...
Donc si tu veux montrer qu'une suite est géométrique il faut calculer le quotient de deux termes consécutif, et montrer qu'il est constant ! (et au passage tu as obtenu la raison...)
L'avantage de cette méthode est qu'elle est systématique...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Non... :/
Si on utilise cette méthode il faut prouver que la suite est non nulle en tous ses termes, ce qui est loin d'être montré ici.
En fait, ce rapport est presque inutile dans la mesure où la plupart du temps montrer que la suite est géométrique (surtout quand ladite suite est définie sur la base d'une autre) se résume à une simple astuce, comme c'est précisément le cas ici =)
Si on utilise cette méthode il faut prouver que la suite est non nulle en tous ses termes, ce qui est loin d'être montré ici.
En fait, ce rapport est presque inutile dans la mesure où la plupart du temps montrer que la suite est géométrique (surtout quand ladite suite est définie sur la base d'une autre) se résume à une simple astuce, comme c'est précisément le cas ici =)
Si on utilise cette méthode il faut prouver que la suite est non nulle en tous ses termes, ce qui est loin d'être montré ici.
Une suite géométrique est de la forme
Comme dans 100% des cas, la suite ne sera pas nulle (aucun intérêt), la technique est légitime (si t'es parano, tu peux toujours calculer dans notre cas v_1 qui est bien non nulle
Tiens, je ne m'étais jamais posé cette question !
On m'avait toujours dit ça, et puis je m'étais aussi rendue compte que calculer ce rapport était souvent très lourd et peu pratique (comme ici, qu'est-ce que cela donnerait ?).
J'en ai fini par me dire que la technique "fonctionnelle" (trouver un k tel que v_{n+1} = k*v_n) était toujours la plus simple et la plus efficace.
Alors dans ce cas je m'excuse :)
On m'avait toujours dit ça, et puis je m'étais aussi rendue compte que calculer ce rapport était souvent très lourd et peu pratique (comme ici, qu'est-ce que cela donnerait ?).
J'en ai fini par me dire que la technique "fonctionnelle" (trouver un k tel que v_{n+1} = k*v_n) était toujours la plus simple et la plus efficace.
Alors dans ce cas je m'excuse :)
Aloha,
Ben le problème ici, c'est que tu sais pas que v_n est géométrique, puisque tu veux le montrer. Donc tu sais pas que les termes sont non nuls. A moins de faire une récurrence pour montrer que les termes sont non nuls, c'est délicat de diviser par v_n.
Zweig a écrit:Une suite géométrique est de la forme, si cette suite est nulle en une valeur de
, elle l'est donc partout car on doit avoir
comme
pour tout
si la raison est non nulle (ou bien
si on commence à 1, dans ce cas
). Dans tous les cas,
doit être la suite nulle.
Comme dans 100% des cas, la suite ne sera pas nulle (aucun intérêt), la technique est légitime (si t'es parano, tu peux toujours calculer dans notre cas v_1 qui est bien non nulle)
Ben le problème ici, c'est que tu sais pas que v_n est géométrique, puisque tu veux le montrer. Donc tu sais pas que les termes sont non nuls. A moins de faire une récurrence pour montrer que les termes sont non nuls, c'est délicat de diviser par v_n.
« Je ne suis pas un numéro, je suis un homme libre ! »
Rebelle : j'avoue ne pas avoir regardé ici ce que donnerais le quotient. Il est plus propre (pour des questions de divisions par zéro, etc...) de trouver le k dont tu parles. La question est : quel est ce k ? (surtout quand la suite est un peu compliquée) Effectuer un rapport, même si c'est compliqué, pas très élégant, etc. c'est systématique. Quand tu ne sais pas quoi faire c'est ce qu'il faut essayer... Quitte lors de la rédaction à factoriser.
En général je distingue trois types de méthodes :
- celles qui sont élégantes et astucieuses. En général rapides elles nécessitent de l'intuition.
- les systématiques. Généralements brutales elles ont pour avantage de ne pas avoir à se poser de question.
- les "non rigoureuses". Elles servent, au brouillon, à trouver des contre-exemples, ou des trucs pour factoriser...
Ici il s'agit d'une méthode systématique, plus ou moins non rigoureuse.
En général je distingue trois types de méthodes :
- celles qui sont élégantes et astucieuses. En général rapides elles nécessitent de l'intuition.
- les systématiques. Généralements brutales elles ont pour avantage de ne pas avoir à se poser de question.
- les "non rigoureuses". Elles servent, au brouillon, à trouver des contre-exemples, ou des trucs pour factoriser...
Ici il s'agit d'une méthode systématique, plus ou moins non rigoureuse.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Pour moi cette méthode dite systèmatique est - particulièrement ici - peu efficace. Celle qui consiste à déterminer ce fameux k se fait presque de tête ou permet en tout cas de rédiger tout ça très rigoureusement en trois lignes ^^'
Enfin, pour ce cas précis elle marche très bien, après je conçois très bien qu'il y ait sûrement des cas où elle ne soit pas la meilleure :)
Enfin, pour ce cas précis elle marche très bien, après je conçois très bien qu'il y ait sûrement des cas où elle ne soit pas la meilleure :)
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
