Spectre d'une projection

[Cryptocatron-11]

BJ ,

Il est marqué sur mon cahier que pour que p soit un projecteur, il faut et il suffit que Sp(p)={0,1} et que p soit diagonalisable.

Ce n'est même pas expliqué pourquoi et je n'arrive pas à comprendre ce pourquoi.

Merci pour votre coup de main :happy2:

[Cryptocatron-11]

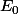
Ah non du coup c'est bon. Parce-que p(u)=1.u donne = F et p(u)=0.u donne = G.

J'avais oublié de préciser que p(u)=v et u=v+w.
Donc si p(u)=0*u v=0 d'ou v=w
Maintenant si p(u)=1*u v=v+w => v=0 et donc u = v

là je pense que c'est bon

[MacManus]

Bj
si p est un projecteur alors il vérifie la propriété suivante p²=p , cad p(p-1)=0.
On dit que le polynôme X(X-1) est le polynôme anulateur de p (polynôme minimal ici).
Pour un espace euclidien E de dimension finie n et F un sous-espace de dimension k de E, la matrice de p est de la forme

[MacManus]

en fait la décomposition que tu donnes peut s'écrire de la manière suivante:
pour tout u de E, p(u) est un élément de F tel que u-p(u) appartient à l'orthogonal de F et on écrit
u = p(u) + u-p(u) (somme directe)

p(u) appartient à F=Im(p)
u-p(u) appartient à (l'orthogonal de F) = Ker(p)

[MacManus]

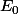
Ah non du coup c'est bon. Parce-que p(u)=1.u donne = F et p(u)=0.u donne = G.

J'avais oublié de préciser que p(u)=v et u=v+w.
Donc si p(u)=0*u v=0 d'ou v=w
Maintenant si p(u)=1*u v=v+w => v=0 et donc u = v

là je pense que c'est bon

p(u)=0 équivaut à dire que v=0, cad u=w=u-p(u)
p(u)=u équivaut à dire que u=u+w, cad w=0=u-p(u)

mais tu l'avais bien compris j'imagine !