Euler07 a écrit:1) Est ce que = B d'après les notations ?
Non je ne sais pas où tu es allé le chercher.
Le texte définit A^-1 à partir de A, puis B = A union A-1, puis H à partir de B, puis il explique pourquoi H = . A aucun moment il y a le moindre truc qui pourrait laisser penser que a une quelconque raison d'être B.
2) La définition de A^-1 ok avec y de G tel que y^-1 est dans A, mais pourquoi c'est aussi égale à l'ensemble {x^-1, tel que x est dans A} ?
Si tu notes i l'opération x -> x^-1 qui va de G dans G, {i(x) / x dans A} est une notation à éviter pour désigner l'image de A par la fonction i, c'est à dire {y de G / il existe x dans A tel que y=i(x)}
Maintenant il faut juste se rendre compte que pour tout y de G,
i(y) est dans A il existe x dans A tel que y=i(x).
Et ça vient du fait que i est une involution de G (pour tout x de G, i(i(x)) = x).
Si i(y) est dans A, alors il existe bien un x=i(y) dans A tel que y=i(x) puisque y=i(i(y)).
Réciproquement, si il existe x dans A tel que y=i(x) alors i(y)=i(i(x)) = x, qui est dans A.
3) Je n'est pas compris le principe de la relation x * y (la transformation avec
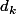
)
* est la loi du groupe (G,*).
Les dk sont là pour dire que si tu prends un produit de n éléments de B, et que tu le multiplies avec un produit de p éléments de B, alors tu obtiens un produit de (n+p) éléments de B.

