Salut, un résultat utile pour déterminer les sous groupes compacts de Gln(R) est le suivant :
Théorème: Soit E un R espace vectoriel de dimension finie. Soit G un sous groupe compact de Gl(E). Soit K une partie convexe, compacte, non vide de E. On suppose que pour tout u dans G, u(K) est contenu dans K (les éléments de G laissent stables K).
Alors il existe x dans K tel que pour tout u dans G, u(x)=x.
Je me demandais, peut on démontrer assez facilement que sous ces hypothèses, on a deja existence d'un point fixe pour tout élément de G? (pas forcément un point fixe commun à tous les éléments de G).
Sous groupe compacts de Gln
13 messages
- Page 1 sur 1
Re: Sous groupe compacts de Gln
Ben 0 est toujours un point fixe de tout le monde.
Si tu cherches des points fixes de f dans K, j'imagine que tu peux regarder un truc comme la moyenne de cesaro de la suite des itérés par f d'un point de K au hasard.
Si tu cherches des points fixes de f dans K, j'imagine que tu peux regarder un truc comme la moyenne de cesaro de la suite des itérés par f d'un point de K au hasard.
Re: Sous groupe compacts de Gln
Tu veux un point fixe dans  , je suppose ?
, je suppose ?
Considère un point de à distance minimum de l'origine (pour un produit scalaire invariant par tous les éléments de
à distance minimum de l'origine (pour un produit scalaire invariant par tous les éléments de  ).
).
Considère un point de
Re: Sous groupe compacts de Gln
Ma question n'était pas de trouver un point fixe commun à tout le monde mais plutôt de montrer que pour u dans G, il existe x dans K tel que u(x)=x.
Pseudo modifié : anciennement Trident2.
Re: Sous groupe compacts de Gln
Oui mais ma question était justement: "comme on cherche à prouver le moins,n'y a-t-il pas un moyen de trouver une preuve moins difficile que celle qu'on utilise pour prouver le plus ?"
Pseudo modifié : anciennement Trident2.
Re: Sous groupe compacts de Gln
Pourquoi chercher à prouver le moins ? A quoi cela avance-t-il ?
Lemme de Kakutani. Soit un sous-groupe compact de
un sous-groupe compact de ) ,
,  un compact convexe non vide de
un compact convexe non vide de  globalement invariant par
globalement invariant par  .
.
Alors a un point fixe dans
a un point fixe dans  .
.
On fixe une norme euclidienne sur
sur  , et on définit
, et on définit 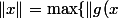 \Vert_0 \;;\; g \in G\}) (bien défini car
(bien défini car  est compact). C'est une norme sur
est compact). C'est une norme sur  , invariante par
, invariante par  ; on a bien
; on a bien  , avec égalité seulement si
, avec égalité seulement si  et
et  sont sur la même demi-droite vectorielle. Alors il y a un unique
sont sur la même demi-droite vectorielle. Alors il y a un unique 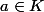 avec
avec  minimum, et
minimum, et  est fixe par
est fixe par  .
.
Lemme de Kakutani. Soit
Alors
On fixe une norme euclidienne
Re: Sous groupe compacts de Gln
Je pense que je me suis fait mal commprendre.
Je connais le lemme de Kakutani ainsi que sa demo. Mais moi quand je lis ce théorème je me dis "mais pourquoi déjà individuellement, chaque élément à un point fixe, ya t-il un argument simple qui permet de le montrer ?"
Je connais le lemme de Kakutani ainsi que sa demo. Mais moi quand je lis ce théorème je me dis "mais pourquoi déjà individuellement, chaque élément à un point fixe, ya t-il un argument simple qui permet de le montrer ?"
Pseudo modifié : anciennement Trident2.
Re: Sous groupe compacts de Gln
Tu ne trouves pas que la démonstration du lemme de Kakutani est simple ? Alors pourquoi chercher ailleurs un résultat moins général dont la démonstration ne sera pas plus simple ?
L'hypothèse de compacité est bien sûr cruciale. Pour un élément isolé de) , il faudrait mettre l'hypothèse que le groupe qu'il engendre est relativement compact. Franchement, je ne vois pas ce qu'on y gagnerait et je ne comprends absolument pas où tu veux en venir.
, il faudrait mettre l'hypothèse que le groupe qu'il engendre est relativement compact. Franchement, je ne vois pas ce qu'on y gagnerait et je ne comprends absolument pas où tu veux en venir.
Si tu veux me convaincre de la pertinence de ton questionnement, tu n'as qu'à trouver une démonstration plus simple que celle que j'ai donnée pour un sous-groupe compact.
L'hypothèse de compacité est bien sûr cruciale. Pour un élément isolé de
Si tu veux me convaincre de la pertinence de ton questionnement, tu n'as qu'à trouver une démonstration plus simple que celle que j'ai donnée pour un sous-groupe compact.
Re: Sous groupe compacts de Gln
Ok, je voulais juste savoir si on pouvait s'entire facilement que chaque élément de G a un point fixe sans passer par Kalutani mais visiblement ce n'est pas le cas.
Pseudo modifié : anciennement Trident2.
Re: Sous groupe compacts de Gln
si tu prends x dans K et g dans G, la suite (un) = (x, (x+g(x))/2, (x+g(x)+g(g(x)))/3, ...) est une suite à valeurs dans K donc a une valeur d'adhérence y. Comme |g(un)-un| est un O(1/n) (K est borné), on a en passant à la limite que g(y)=y.
Mais bon la preuve du lemme m'a pas l'air très compliquée non plus.
Mais bon la preuve du lemme m'a pas l'air très compliquée non plus.
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
