Sommes de Riemann
23 messages
- Page 1 sur 2 - 1, 2
Sommes de Riemann
Bonjour chers amis,
Svp j'ai une petite question sur les sommes de Riemann.
On dit que lim[(b-a)/n]∑f(aᵢ+i/n) i ---› 1 à n = intégrale de a à b de f(x)dx
J'aimerais savoir pourquoi l'on a tendance à travailler sur [0, 1] ?
Merci d'avance !
Svp j'ai une petite question sur les sommes de Riemann.
On dit que lim[(b-a)/n]∑f(aᵢ+i/n) i ---› 1 à n = intégrale de a à b de f(x)dx
J'aimerais savoir pourquoi l'on a tendance à travailler sur [0, 1] ?
Merci d'avance !
Re: Sommes de Riemann
Bonjour
Pour la simple raison, c'est que tu peux toujours faire un changement de variable affine qui te ramène
un intervalle [a,b] à [0,1].
Pour les neurones on aime bien ne pas les fatiguer et travailler sur un même intervalle de référence.
C'est un peu la même chose pour les limites, DSE, .... on aime bien travailler en 0.
Si tu cherches le comportement d'une fonction en x=1 tu poses u=x-1 et tout revient à calculer en u=0.
Pour les éléments finis c'est idem. N'importe quel triangle du maillage tu le ramènes à un triangle dit de référence où on sait bien calculer.
En maths il n'y a que ça, on fait des transformations aussi simples que possible pour se ramener où on est à l'aise.
Pour la simple raison, c'est que tu peux toujours faire un changement de variable affine qui te ramène
un intervalle [a,b] à [0,1].
Pour les neurones on aime bien ne pas les fatiguer et travailler sur un même intervalle de référence.
C'est un peu la même chose pour les limites, DSE, .... on aime bien travailler en 0.
Si tu cherches le comportement d'une fonction en x=1 tu poses u=x-1 et tout revient à calculer en u=0.
Pour les éléments finis c'est idem. N'importe quel triangle du maillage tu le ramènes à un triangle dit de référence où on sait bien calculer.
En maths il n'y a que ça, on fait des transformations aussi simples que possible pour se ramener où on est à l'aise.
Re: Sommes de Riemann
Ok merci
Mais souvent il arrive que i ---› n à 2n-1. J'aimerais savoir si l important est de garder le nombre de termes = n ?
Merci.
Mais souvent il arrive que i ---› n à 2n-1. J'aimerais savoir si l important est de garder le nombre de termes = n ?
Merci.
Re: Sommes de Riemann
Effectivement comme tu le vois il faut se ramener à des trucs standard
Tu poses
Donc ta somme S_n est!
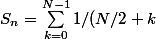=1/N \sum_{k=0}^{N-1} 1/(1/2+k/N)=1/N \sum_{k=0}^{N-1} f(k/N))
où=1/(1/2+x))
D'où la limite c'est dx) facile à calculer
facile à calculer
Tu poses
Donc ta somme S_n est!
où
D'où la limite c'est
Re: Sommes de Riemann
Bon ok Yezu j'ai répondu avec k=0.
Dans ce cas
tu poses k'=n-k et tu mets 1/n en facteur et regardes cela devrait aller
Dans ce cas
tu poses k'=n-k et tu mets 1/n en facteur et regardes cela devrait aller
Re: Sommes de Riemann
En fait j'avais déjà calculer.
Mais si tu poses N = 2 * n , comment tu trouves k = 0 ?
Selon moi si on pose N = 2 * n alors n = N / 2 , mais le calcul devient un peu compliqué
Mais si tu poses N = 2 * n , comment tu trouves k = 0 ?
Selon moi si on pose N = 2 * n alors n = N / 2 , mais le calcul devient un peu compliqué
Re: Sommes de Riemann
Salut, si Yezu à raison :
Pour la résoudre tu peux imaginer que est presque continue quand
est presque continue quand  tend vers
tend vers  ;
;
Donc tu peux poser une intégrale:

Pour la résoudre tu peux imaginer que
Donc tu peux poser une intégrale:
Modifié en dernier par FLBP le 17 Aoû 2018, 18:32, modifié 1 fois.
Re: Sommes de Riemann
C'est pas ça du tout. Comme tu n'a pas mis k=n j'ai cru comprendre que l'exercice c'est k=0 à.....
J'ai fais un calcul en fonction de cela.
Mais maintenant si k=n à ... c'est différent il faut poser k'=k-n
ainsi k' va de 0 à n-1 c'est une autre question mais tu retombes sur une somme de Riemann standard
J'ai fais un calcul en fonction de cela.
Mais maintenant si k=n à ... c'est différent il faut poser k'=k-n
ainsi k' va de 0 à n-1 c'est une autre question mais tu retombes sur une somme de Riemann standard
Re: Sommes de Riemann
Bonjour @FBLP la question de @georges c'est comment on se ramène à une somme de Riemann standard
de la forme)
je crois qu'il sait que (si f est correct) que cela converge vers dt)
de la forme
je crois qu'il sait que (si f est correct) que cela converge vers
Re: Sommes de Riemann
Georges10 a écrit:Par exemple on demande de calculer lim ∑ 1/(n+k) k ---› n à 2n-1
Bonsoir,
Pour calculer une somme de Riemann, il faut se ramener à
Dans ton exemple pour s'y ramener, il faut poser
23 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
