Sommes de Riemann
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
 par Kolis » 18 Aoû 2018, 09:04
par Kolis » 18 Aoû 2018, 09:04
Bonjour !
Vous avez raison si vous voulez absolument vous ramener à une somme de Riemann.
Mais pour étudier juste la suite je préfère écrire
}\dfrac1{k+n}=H_{3n}-H_{n-1})
où
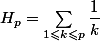
et terminer par
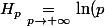+\gamma+o(1/p))
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 18 Aoû 2018, 09:58
par Pseuda » 18 Aoû 2018, 09:58
Bonjour,
@Kolis, c'est dans le cas où on connait la suite
)
(série harmonique) et la convergence de la suite
))
vers la constante d'Euler.
Sinon, la somme c'est
 - H(2n-1))
.
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
 par Kolis » 18 Aoû 2018, 14:56
par Kolis » 18 Aoû 2018, 14:56
Les écritures non-latex étant assez floues j'ai pris l'indice entre

bornes comprises.
Si on veut s'arrêter à
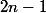
tu as raison.
Pour le
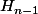
j'ai bien fait une erreur !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités