Sommes de Riemann et détermination de limite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 11 Mar 2015, 10:53
par ArtyB » 11 Mar 2015, 10:53
Bonjour,
Pour calculer la limite en plus l'infini de:
(1/n)* [Somme de 1 à n de racine n-ième de 2^k]
Je ne sais pas comment insérer une écriture mathématiques ici donc la voici en image:

Je sais que cette somme peut se transformer en intégrale et que cela m'aidera à trouver la limite, mais je ne sais pas du tout comment transforme cette somme en integrale.
Normalement on a Somme de 0 à n-1 de ((Xi+1-Xi)*yi)=integrale mais là...
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 11 Mar 2015, 11:05
par arnaud32 » 11 Mar 2015, 11:05
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 11 Mar 2015, 11:08
par ArtyB » 11 Mar 2015, 11:08
Ah bien vu pour poser ça comme fonction.
Mais lorsqu'on a 1/n Somme de 1 à n de f(k/n) comment transformer ça intégrale ?
Et pourquoi calculer l'integrale entre 0 et plus l'infini de f ?
-
DamX
- Membre Rationnel
- Messages: 630
- Enregistré le: 02 Oct 2012, 13:12
-
 par DamX » 11 Mar 2015, 11:17
par DamX » 11 Mar 2015, 11:17
ArtyB a écrit:Ah bien vu pour poser ça comme fonction.
Mais lorsqu'on a 1/n Somme de 1 à n de f(k/n) comment transformer ça intégrale ?
Et pourquoi calculer l'integrale entre 0 et plus l'infini de f ?
Hello,
C'est entre 0 et 1, pas entre 0 et l'infini, arnaud32 s'est corrigé entre temps.
Et le pourquoi, c'est que c'est une somme de Riemann, une sommation "en rectangles" qui va converger vers l'intégrale :
http://fr.wikipedia.org/wiki/Somme_de_Riemann. Du coup la limite de la somme est exactement égale à l'intégrale (car la fonction f est continue sur [0,1])
Damien
-
DamX
- Membre Rationnel
- Messages: 630
- Enregistré le: 02 Oct 2012, 13:12
-
 par DamX » 11 Mar 2015, 11:33
par DamX » 11 Mar 2015, 11:33
Pour info, on peut calculer la limite autrement, sans utiliser un passage à l'intégrale, car on peut calculer la somme exactement, c'est en fait une somme géométrique classique :
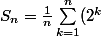^{1/n} = \frac{1}{n}\sum_{k=1}^n(2^{1/n})^k)
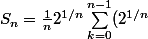^k = \frac{1}{n}2^{1/n}\frac{(2^{1/n})^n-1}{2^{1/n}-1} = \frac{1}{n}\frac{2^{1/n}}{2^{1/n}-1})
Ensuite, pour avoir la limite de cette expression, il suffit de faire un petit développement limité ou un équivalent. En effet :
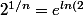/n})
, et tu dois savoir que

lorsque x tend vers 0, ce qui est le cas de ln(2)/n.
Du coup,
}{n})
, et finalement :
}{n}} = \frac{1}{ln(2)})
Tu verras que tu dois retrouver le même résultat que par le passage par l'intégrale.
Damien
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 11 Mar 2015, 11:40
par ArtyB » 11 Mar 2015, 11:40
Merci beaucoup !
Dans mon cours (CNED) pour la somme de Riemann il était seulement dit:
"Somme de 0 à n-1 de ((Xi+1-Xi)*yi)=integrale"
Il ne faisait pas référence à la méthode des rectangles...
Je comprends beaucoup mieux maintenant, merci beaucoup à vous !
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 11 Mar 2015, 11:43
par ArtyB » 11 Mar 2015, 11:43
Du coup on a une primitive F de f:
F(x)=(1/ln(2)) * e^(x*ln(2))
Donc l'intégrale vaut 1/ln(2) et la limite de même ?
EDIT: je n'avais pas vu l'autre façon de faire en calculant directement la somme, merci beaucoup !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 96 invités

