Somme de vecteurs et de sev

[Ben314]

Salut,
Pour toi, c'est quoi la définition de F+G lorsque F et G sont deux sous-espaces vectoriels ?

[Ben314]

C'est bien ça la définition de la somme de deux (ou plus) sous espaces vectoriels : c'est tout les vecteurs que l'on peut écrire sous la forme de la somme de deux (ou plus) termes, le premier dans le premier s.e.v. et le deuxième dans le second.

Par exemple, dans R^2, si F est l'axe des x (=l'ensemble des (x,0)) et G l'axe des y (= l'ensemble des (0,y)) alors F+G c'est tout les vecteurs de la forme (x,0)+(0,y)=(x,y), c'est à dire tout les vecteurs du plan.

Question : si un vecteur (x,y) s'écrit (x',y')+(x",y"), peut on en déduire que les deux vecteurs (x',y') et/ou (x",y") sont sur les axes ?

[Ben314]

Justement, l'exemple que je te donne montre que c'est totalement faux : par exemple le vecteur (3,5) est bien dans F+G vu qu'il s'écrit (3,0)+(0,5).
Mais on peut aussi écrire un truc du style (3,5)=(2,1)+(1,4) et les vecteurs (2,1) et (1,4) ne sont ni dans F, ni dans G !

[Ben314]

Non, il n'est pas nécessaire d'avoir le truc que tu dit.
Si tu prend un vecteur v quelconque de (FnG)+(FnH), il te suffit de savoir qu'il existe des vecteurs v1 et v2 respectivement dans FnG et FnH tels que v=v1+v2 pour que la suite du raisonnement fonctionne.
Le vecteur v en question peut surement aussi s'écrire v=w1+w2 avec w1 et w2 pas du tout dans FnG ni FnH ce qui signifie que la suite du raisonnement ne fonctionnerais pas avec ces vecteurs là, mais... on s'en fout complètement...

Si on te demande de montrer un truc et que tu essaye 36.000 pistes différentes pour le prouver.
Ben il suffit qu'UNE des piste te conduise au résultat pour que tu ait gagné.
Le fait que des tas d'autre pistes ne mènent à rien ne prouve pas que le truc à montrer soit faux (ni qu'il soit vrai d'ailleurs... :zen: )

[Ben314]

Bon, on va prendre un exemple complètement con.

Supposons que l'on te demande de montrer que 5 est la somme de deux entiers positifs.
Le prof, dans la correction, il écrit "5=3+2 donc c'est vrai"
Et toi, tu dit, je comprend pas, on a aussi 5=8+(-3) et -3 n'est pas positif !

[Ben314]

En fait, j'ai l'impression que c'est au départ de la preuve qu'il y a un truc qui t'échappe.

On veut montrer que .
Il faut donc montrer que tout les éléments de l'ensemble de gauche sont des éléments de celui de droite.

On part donc d'un vecteur quelconque .
Par définition de la somme de deux s.e.v., on sait qu'on peut écrire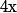 sous la forme avec et (il peut aussi s'écrire de tas d'autres façon, mais on s'en fout, c'est uniquement cette écriture qui nous intéresse)
Là, tu recopie ce que tu as écrit au dessus et tu en déduit que , c'est à dire que

Ca termine la preuve vu que le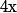 dont on est parti est bien un élément quelconque de