Somme d'une partie entière
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 02 Nov 2019, 15:31
par akiwhite » 02 Nov 2019, 15:31
Bonjour,
je bloque sur l'exercice suivant : Calculer la somme
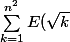})
pour tout n dans N
On nous indique que la somme des k² de 1 a n est égale a n(n+1)(2n+1)/6
Je ne sais pas comment commencer,
merci pour votre aide,
Akiwhite
Modifié en dernier par
akiwhite le 02 Nov 2019, 15:55, modifié 4 fois.
-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 02 Nov 2019, 15:36
par Tuvasbien » 02 Nov 2019, 15:36
Il sert à quoi le x ?
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 02 Nov 2019, 15:38
par akiwhite » 02 Nov 2019, 15:38
Tuvasbien a écrit:Il sert à quoi le x ?
Excusez moi j'ai recopié la fin de l'énoncé d'à côté

-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 02 Nov 2019, 15:46
par Tuvasbien » 02 Nov 2019, 15:46
Ok, mais la question reste incomplète, il faut montrer quoi ?
-
mathelot
 par mathelot » 02 Nov 2019, 15:47
par mathelot » 02 Nov 2019, 15:47
akiwhite a écrit:Je ne sais pas comment commencer,
La somme se calcule,Il s'agit de sommer par paquets
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 02 Nov 2019, 15:47
par akiwhite » 02 Nov 2019, 15:47
Tuvasbien a écrit:Ok, mais la question reste incomplète, il faut montrer quoi ?
Je suis vraiment désolé je suis pas reveillé, c'est corrigé

-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 02 Nov 2019, 15:53
par Tuvasbien » 02 Nov 2019, 15:53
On fait une partition sur les valeurs possibles de

, si
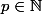
alors
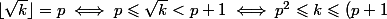^2-1)
. Ainsi
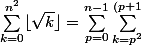^2-1}\lfloor\sqrt{k}\rfloor +\lfloor\sqrt{n^2}\rfloor=\ldots)
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 02 Nov 2019, 16:02
par akiwhite » 02 Nov 2019, 16:02
Tuvasbien a écrit:On fait une partition sur les valeurs possibles de

, si
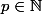
alors
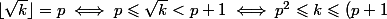^2-1)
.[/tex]
D'ou viens le -1 après p+1 au carré ??
-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 02 Nov 2019, 16:21
par Tuvasbien » 02 Nov 2019, 16:21
S’agissant d’entiers,
^2\iff k\leqslant (p+1)^2 -1)
-
akiwhite
- Membre Naturel
- Messages: 96
- Enregistré le: 22 Sep 2019, 18:36
-
 par akiwhite » 02 Nov 2019, 16:31
par akiwhite » 02 Nov 2019, 16:31
Tuvasbien a écrit:Ainsi
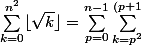^2-1}\lfloor\sqrt{k}\rfloor +\lfloor\sqrt{n^2}\rfloor=\ldots)
Bon et bien je n'ai pas compris pourquoi ca devient la somme de la somme
-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 02 Nov 2019, 16:35
par Tuvasbien » 02 Nov 2019, 16:35
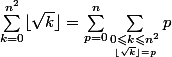
On regroupe les termes selon les valeurs de

, écris la somme avec des points de suspension si tu as du mal.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
, si
alors
.[/tex]