Somme des puissances mièmes des racines nièmes de l'unité !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
max
- Membre Relatif
- Messages: 126
- Enregistré le: 27 Oct 2005, 14:15
-
 par max » 14 Oct 2006, 13:47
par max » 14 Oct 2006, 13:47
Bonjour, je dois montrer que
la somme des puissances mièmes des racines nièmes de 1 est nulle SAUF si n divise m J'ai trouvé que cette somme s'exprimait mathématiquement ainsi (et je pense avoir bon) :
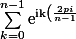} ^m})
Mais je n'arrive pas à le démontrer.
Pourriez vous m'aider ?
Merci
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 14 Oct 2006, 14:42
par alben » 14 Oct 2006, 14:42
bonjour,
Tu as déjà corrigé une erreur de transcription, il te faut également remplacer le diviseur de l'exposant par n au lieu de n-1
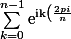} ^m})
Pose p=m/n et remplace les e^i... par des cos et sin, ça te donnera déjà la valeur de la somme lorsque n divise m.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 14 Oct 2006, 14:50
par tize » 14 Oct 2006, 14:50
la somme des puissances mièmes des racines nièmes de 1
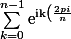} ^m})
c'est pas plutôt :
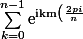}})
?
-
max
- Membre Relatif
- Messages: 126
- Enregistré le: 27 Oct 2005, 14:15
-
 par max » 14 Oct 2006, 14:59
par max » 14 Oct 2006, 14:59
Oui, excusez moi, j'ai fait plein de bétises en recopiant en latex ma formule.
Celle que j'ai vraiment trouvé (et elle est bonne cette fois!) est
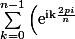^m)
Mais je ne comprends toujours pas comment prouver ce qu'on me demande

-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 14 Oct 2006, 15:02
par tize » 14 Oct 2006, 15:02
max a écrit:Oui, excusez moi, j'ai fait plein de bétises en recopiant en latex ma formule.
Celle que j'ai vraiment trouvé (et elle est bonne cette fois!) est
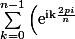^m)
Mais je ne comprends toujours pas comment prouver ce qu'on me demande

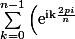^m = \sum_{k=0}^{n-1} \left( {}{\text{e}^{\text{im}{\frac{2pi}{n}}} {} \right)^k)
...somme des termes d'une suite geometrique
-
max
- Membre Relatif
- Messages: 126
- Enregistré le: 27 Oct 2005, 14:15
-
 par max » 14 Oct 2006, 15:33
par max » 14 Oct 2006, 15:33
tize a écrit: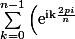^m = \sum_{k=0}^{n-1} \left( {}{\text{e}^{\text{im}{\frac{2pi}{n}}} {} \right)^k)
...somme des termes d'une suite geometrique
oui, c'est ce que j'avais remarqué, mais je ne vois pas quoi faire de la condition "sauf si n divise m"
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 14 Oct 2006, 15:42
par abcd22 » 14 Oct 2006, 15:42
Bonjour,
Essaie de calculer la somme sans te préoccuper de cette condition au départ (tu la verras apparaître en faisant le calcul) :
- si

on a une formule pour les sommes de termes d'une suite géométrique,
- si
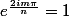
, qu'est-ce que ça veut dire pour m et n ?
-
max
- Membre Relatif
- Messages: 126
- Enregistré le: 27 Oct 2005, 14:15
-
 par max » 14 Oct 2006, 15:45
par max » 14 Oct 2006, 15:45
abcd22 a écrit:Bonjour,
Essaie de calculer la somme sans te préoccuper de cette condition au départ (tu la verras apparaître en faisant le calcul) :
- si

on a une formule pour les sommes de termes d'une suite géométrique,
- si
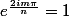
, qu'est-ce que ça veut dire pour m et n ?
Je trouve, dans le cas où
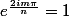
, que la somme est égale à n (et donc différente de 0). J'ai bon?
edit: et, bien sur,
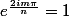
quand m=n*q, c'est à dire quand n divise m, ce qui donne donc exp(i.q.2pi)=1)
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 14 Oct 2006, 15:54
par abcd22 » 14 Oct 2006, 15:54
Oui c'est bon !
-
max
- Membre Relatif
- Messages: 126
- Enregistré le: 27 Oct 2005, 14:15
-
 par max » 14 Oct 2006, 15:54
par max » 14 Oct 2006, 15:54
Voilà, je trouve bien que la somme de ...... est égale à 0 quand n ne divise pas m.
J'ai encore une petite question :) exp(i.m.2pi)=1 (m entier naturel), c'est évident, ou il faut écrire une petite phrase qui l'explicite?
Merci beaucoup de votre aide.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 14 Oct 2006, 15:56
par tize » 14 Oct 2006, 15:56
max a écrit:Voilà, je trouve bien que la somme de ...... est égale à 0 quand n ne divise pas m.
J'ai encore une petite question

exp(i.m.2pi)=1 (m entier naturel), c'est évident, ou il faut écrire une petite phrase qui l'explicite?
Merci beaucoup de votre aide.
Il y a un i en trop...!
sinon je trouve ça plutôt evident mais ça doit dependre du niveau....
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
on a une formule pour les sommes de termes d'une suite géométrique,
, qu'est-ce que ça veut dire pour m et n ?
exp(i.m.2pi)=1 (m entier naturel), c'est évident, ou il faut écrire une petite phrase qui l'explicite?