Somme des inverses des carrés

par **Othman** » 08 Mai 2019, 13:01

Bonjour tout le monde,
pourriez vous svp m'aider à montrer que :

sachant que :

et que les

sont des réels deux à deux distincts

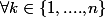
et qu'à l'aide du coefficient de

Merci beaucoup pour vos réponses

par **Sa Majesté** » 08 Mai 2019, 15:17

Salut

Il suffit ensuite de développer

et de ne garder que les termes de puissance impaire pour trouver la partie imaginaire.

par **Othman** » 08 Mai 2019, 15:30

J'ai corrigé l'expression, le 1/2i est facteur de tout le reste

par **Sa Majesté** » 08 Mai 2019, 19:46

C'est bien comme ça que je l'avais compris 8-)

par **Othman** » 08 Mai 2019, 22:28

j'ai du mal à comprendre pourquoi c'est la partie imaginaire que de

par **noobey** » 09 Mai 2019, 10:03

Hello!

par **Othman** » 09 Mai 2019, 16:41

Merci c'est clair maintenant