Singleton est un fermé

[mploki]

Un singleton est un fermé ? Doit on le prouver si on l'utilise dans un exercice ? Si oui, comment ?

[Nightmare]

Salut,

ne penses-tu pas qu'il manque des précisions pour répondre à la question?

[mploki]

Salut,

ne penses-tu pas qu'il manque des précisions pour répondre à la question?

D'accord, je voudrai juste savoir si j'ai le droit de déduire qu'un singleton est un fermé, ou ai je à le prouver ?

[girdav]

Il faut commencer par définir sur quel ensemble on se place, et de quelle topologie il est muni.

[Nightmare]

D'accord, je voudrai juste savoir si j'ai le droit de déduire qu'un singleton est un fermé, ou ai je à le prouver ?

Je ne comprends pas ta réponse. Si tu es d'accord qu'il manque des données, pourquoi ne les fournis-tu pas plutôt que de reposer exactement la même question avec toujours autant de données manquantes?

[mploki]

J'étudie des matrices de M;)(IK), mais moi je pose la question plus généralement.
De quelle topologie il est muni, ça je ne comprends pas. :triste:

Et je n'arrive pas à voire ce qu'il manque comme donnée, j'aimerai comprendre si un singleton est obligatoirement un fermé, quelque soit l'ensemble ou je me place.

[lapras]

J'étudie des matrices de M;)(IK), mais moi je pose la question plus généralement.
De quelle topologie il est muni, ça je ne comprends pas. :triste:

Et je n'arrive pas à voire ce qu'il manque comme donnée, j'aimerai comprendre si un singleton est obligatoirement un fermé, quelque soit l'ensemble ou je me place.

Salut,
est ce que tu as fait de la topologie générale (i.e en définissant la topologie par ses ouverts) ?
Si oui, une condition suffisante pour qu'un espace topologique X soit tel que ses singletons sont fermés est la suivante : X est séparé (i.e pour tous x différent de y, il existe un voisinage Vx de x et un voisinage Vy de y tels que Vx et Vy ne s'intersectent pas).

Si tu n'as fait de la topologie que dans les espaces normés (ou mieux : métriques), alors les singletons sont toujours fermés. Ca vient du fait que si x est un point de ton espace, si tu prends le complémentaire du singleton x, il est immédiatement ouvert (tout point est le centre d'une boule n'intersectant pas x).

[alm]

Salut,

Je crois que le cadre de travail pour mploki ne depasse pas les evn (espaces vectoriels normés)

Auquel cas , oui tout sigleton est un fermé et ne t'amuse pas à le démontrer car c'est du cours..

Tu as plus : toute partie finie d'un evn est un fermé

Pour démontrer q'un singleton est fermé il suffit de distinguer deux cas :

Si notre espace (appelons le et sa norme ) est nul : il y a un unique singleton et il est fermé car égal à

Sinon soit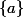 un tel singleton et tel que .
alors la boule ouverte vérifie: ; d'où le résultat par définition d'un fermé ...

[maxi1989]

Un singleton est un fermé ? Doit on le prouver si on l'utilise dans un exercice ? Si oui, comment ?

Tout dépend de la topologie de ton espace. Mais si ton espace est de Hausdorff, alors oui un singleton est toujours fermé

[mploki]

Merci Merci :we:
Et effectivement, je n'ai fait de la topologie que dans des espaces vect normés.
Merci encore !