Simplification de produits

par **Help19** » 27 Déc 2009, 13:25

Bonjour

J'ai un DL à rendre pour la rentrée et je bloque sur deux petites questions.
La question est de simplifier les expressions Pn et Qn (probablement trouver une formule qui permet d'obtenir Pn n )

J'ai développé le premier, Pn, et je constate que:
P2 = 3/4
P3 = 2/3
P4 = 5/8
.
.
.
Pn = 3/4 * 2/3 * 5/8 * ... * (1 - 1/n²)

Je pense qu'il faut procéder en démontrant par récurrence une formule (à base de factorielles peut être) qui puisse permettre d'obtenir Pn n

Pour Qn, je n'ai encore rien tenté mais je vais essayer tout de suite ...
Merci d'avance

par **Ericovitchi** » 27 Déc 2009, 13:41

Pour le premier

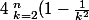Tu écris

Ca te ramène à calculer 3 produits qui sont faciles à exprimer avec des factorielles.

par **Help19** » 27 Déc 2009, 13:43

Merci pour ta réponse, je vais faire ça ;)

par **Ericovitchi** » 27 Déc 2009, 13:49

Pour le second exprimes les deux coefficients sous forme de factorielles, ça se simplifie beaucoup et tu es ramené à un produit très simple à exprimer.

par **Help19** » 27 Déc 2009, 13:58

Merci beaucoup.
Sinon, pour Pn, j'ai trouvé une autre méthode aussi qui m'a l'air pas trop mal.
On calcule les premiers termes comme je l'ai fait (P2 = 3/4, P3 = 2/3 ...)
On se rend compte que Pn peut se mettre sous la forme (n+1)/2n
On démontre ensuite cette formule avec une démonstration par récurrence ...

Je vais m'occuper de Qn tout de suite ;)

par **Help19** » 27 Déc 2009, 14:31

Voilà, j'ai terminé la simplification de Pn en démontrant par récurrence que la formule Pn = (n+1)/2n est vraie

Maintenant, pour Qn, je trouve ceci:

C'est terminé ou il faut que je procède comme pour Pn, en démontrant par récurrence une formule qui puisse permettre de trouver Qn quelque soit n appartenant à N ?

par **Ericovitchi** » 27 Déc 2009, 15:14

Pour Qn tu peux sortir le n+1 du produit. Et puis le produit de 1(n-k) c'est le même que le produit de 1/k, il suffit de parcourir les indices dans l'autre sens

par **Help19** » 27 Déc 2009, 15:25

Peut-on vraiment sortir (n + 1) ? Ce n'est pourtant pas une constante :hein:

par **girdav** » 27 Déc 2009, 15:37

C'est une constante en

: tant que ça ne dépend pas de la variable de sommation c'est bon.

par **Help19** » 27 Déc 2009, 15:39

D'accord.
Bon entre temps, j'ai trouvé que Qn = n!

Ca vous semble correct ?

par **Help19** » 27 Déc 2009, 15:46

Ah non, ça marche pas en fait :briques:

par **girdav** » 27 Déc 2009, 15:46

Si ce que tu as fais au message #6 est correct (je n'ai pas vérifié), alors ce résultat n'est pas correct.
On devrais avoir une fraction avec de la factorielle au dénominateur.

par **Help19** » 27 Déc 2009, 15:46

Ouais c'est ce que je viens de constater. Qn n'est pas égal à n! en fait xD

par **girdav** » 27 Déc 2009, 15:47

Et si tu parcourais le produit dans "l'autre sens"?

par **Help19** » 27 Déc 2009, 15:47

Ok je vais faire ça
Merci

par **Help19** » 27 Déc 2009, 15:52

Ca ferait donc:
Qn = (n+1)/n!

C'est bon ?

Edit: c'est pourtant faux lorsque je calcule Q2 et que je le compare avec le résultat de la formule initiale Qn ...

par **girdav** » 27 Déc 2009, 15:54

En se basant sur #6 oui.
Edit dans ce cas utilise

dans l'expression de

.

par **Help19** » 27 Déc 2009, 15:58

Ok
Mais quand je vérifie, je trouve Q2 = 9/2 avec la toute première formule
Et avec la formule #6 (ou Qn = (n+1)/n! peut importe), je trouve Q2 = 3/2

Bizarre ...

par **Help19** » 27 Déc 2009, 15:59

girdav a écrit:Edit dans ce cas utilise
dans l'expression de .

Ouais, j'ai fait cela justement, à partir de la première formule

Edit: J'ai refait tous mes calculs, et je suis sur à 100 % que Qn = (n+1)/n!
Y a pas d'erreur possible, c'est forcément ça :mur:

par **sniperamine** » 27 Déc 2009, 16:14

Help19 a écrit:Ouais, j'ai fait cela justement, à partir de la première formule

Edit: J'ai refait tous mes calculs, et je suis sur à 100 % que Qn = (n+1)/n!
Y a pas d'erreur possible, c'est forcément ça :mur:

Ben non tu as fait une erreur c'st (n+1)^n

Simplification de produits

Simplification de produits

Qui est en ligne