Complexes,calculs produits de sinus
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
d.masse3
- Membre Naturel
- Messages: 10
- Enregistré le: 10 Nov 2006, 11:00
-
 par d.masse3 » 22 Avr 2007, 13:26
par d.masse3 » 22 Avr 2007, 13:26
bonjours à celles et ceux qui viennent lire ce message; j'ai une difficulté à démarer un exercice:il s'agit de calculer
produit des sin(a+kpi/n) k variant de 1 à (n-1), a quelconque
merci d'avance
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 22 Avr 2007, 14:24
par tize » 22 Avr 2007, 14:24
Bonjour,
Soit l'équation :
^n=e^{i2na})
Trouve les racines
_{1\leq k\leq n})
ensuite sers toi du fait que dans un polynôme unitaire le produit des racines est égal au terme constant à un signe près.
-
d.masse3
- Membre Naturel
- Messages: 10
- Enregistré le: 10 Nov 2006, 11:00
-
 par d.masse3 » 22 Avr 2007, 14:55
par d.masse3 » 22 Avr 2007, 14:55
est- ce que mes racines sont exactes?
[zk=e^i(2a+kpi/n)-1]
je sais que la somme des racinnes nieme est égale à 0, mais d'emblée je ne vois pas le produit égal au terme constant...
j'essaie avec n=2
merci, déja pour la piste.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 22 Avr 2007, 20:01
par tize » 22 Avr 2007, 20:01
Bonsoir,
^n=e^{i2na})
donc

avec k=0;1;...;n-1. donc
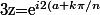}-1 = e^{i(a+k\pi/n)}\(e^{i(a+k\pi/n)}-e^{-i(a+k\pi/n)}\)=2ie^{i(a+k\pi/n)}\sin(a+k\pi/n))
-
d.masse3
- Membre Naturel
- Messages: 10
- Enregistré le: 10 Nov 2006, 11:00
-
 par d.masse3 » 22 Avr 2007, 23:05
par d.masse3 » 22 Avr 2007, 23:05
est ce que la solution est du type:
(-1)^(n-1)*2^(1-n)*sin(na)
je ne suis pas très sur de mes simplifications.
merci, beaucoup José
cordialement
Dominique
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 23 Avr 2007, 12:08
par tize » 23 Avr 2007, 12:08
Bonjour,
pour la solution finale, je trouve :
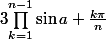=\frac{\sin(na)}{2^{n-1}\sin(a)})
ou si le produit commence en k=0:
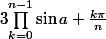=\frac{\sin(na)}{2^{n-1}})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
