Séries Taylor et dérivées successives
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Yezu
- Membre Relatif
- Messages: 335
- Enregistré le: 14 Fév 2018, 12:29
-
 par Yezu » 02 Juil 2018, 08:38
par Yezu » 02 Juil 2018, 08:38
Bonjour à tous,
Je viens de commencer le chapitre sur les DL et séries de Taylor dans mon bouquin et j'aurais une petite question sur la méthode pour trouver les dérivées succesives.
Quand on dit de montrer par exemple qu'il existe
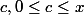
:
 = \sum_{k=1}^{n-1} \frac{(-1)^{k-1} x^k}{k} + \frac{(-1)^{n-1}}{n} (\frac{x}{1+c})^n)
.
Par tatonnement, j'arrive à une formule pour les dérivées successives de
 = \ln (x))
:
} (x) = \frac{(-1)^{k-1} (k-1)!}{x^k})
.
Je pense qu'il faut le montrer par récurrence mais existe-il une autre méthode ?
Merci d'avance.
-
aviateur
 par aviateur » 02 Juil 2018, 11:24
par aviateur » 02 Juil 2018, 11:24
En utilisant les propriétés relatives au chapitre alors
pour ce DL on passe par la dérivée: 1/(1+x) dont le développement de Taylor est bien connu
(série géométrique)
1/(1+x)=1-x+x^2+x^3....
Donc en intégrant tu obtiens le DL de
=x-x^2/2+x^3/3-.......+(-1)^{n+1} x^n/n +o(x^n))
au voisinage de 0.
-
Yezu
- Membre Relatif
- Messages: 335
- Enregistré le: 14 Fév 2018, 12:29
-
 par Yezu » 02 Juil 2018, 11:40
par Yezu » 02 Juil 2018, 11:40
Merci beaucoup pour ta réponse aviateur !
Dans le bouquin, ils font malheureusement tout ce qui est Taylor avant les DL ):
Cette méthode est assez immédiate, cependant ça tombe bien ici avec la série géométrique; pour le calcul de séries qui ne "tombent pas bien", existerait-il d'autres méthodes à part le tatonnement-récurrence pour trouver les dérivées successives ?
-
aviateur
 par aviateur » 03 Juil 2018, 12:31
par aviateur » 03 Juil 2018, 12:31
Ce qu'il se passe quand tu étudies les développement limités, les développement en séries entières, les formules de Taylor....
bien que tout cela soit bien différents (et il faut bien connaître son cours pour cela) il y a un point communs c'est la partie polynomiale que l'on obtient par calculs avec des techniques opératoires basées sur les propriétés de cours.
Mais il y a les classiques (e^x, sin(x),cos(x), 1/(1-x) ln(1-x),(1+x)^a ....) dont la partie polynomiale est justifiée dans tout cours normalement constitué.
Le mieux est de revoir comment on obtient ces classiques, et, pour le reste c'est assez vaste donc difficile d'indiquer une méthode. Mais la plupart du temps, modulo quelques petites manipulations, on revient toujours sur ces classiques. Le mieux étant de faire quelques exercices de calculs.
-
Yezu
- Membre Relatif
- Messages: 335
- Enregistré le: 14 Fév 2018, 12:29
-
 par Yezu » 03 Juil 2018, 13:11
par Yezu » 03 Juil 2018, 13:11
Merci bien pour ta réponse aviateur.
Ce n'est pas évident (pour ma personne) de suivre un cours brut sans astuces de la part de prof/exemples, etc.
Merci beaucoup encore de me permettre de combler mes manquants !
Cordialement,
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
