Dérivées successives !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 03 Jan 2010, 15:27
par barbu23 » 03 Jan 2010, 15:27
Bonjour à tous :
On note :
 $)
l'ensemble des racines

-ièmes de l'unité.
Dans toute la suite :

étant un entier naturel fixé:
Soit :
 \in \mathbb{N}^{m} $)
:
Soit :
 \in \mathbb{U}(n_{1}) \times \ldots \times \mathbb{U}(n_{m}) $)
:
On pose :
 = e^{a_{1} x} + e^{a_{2} x} + \ldots + e^{a_{m} x} $$)
Alors :
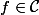
Question :
Existe-t-il
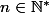
tel que :
}(x) = f(x) $)
i.e :
Existe-t-il
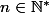
tel que :
} = f $)
Merci d'avance
-
SlowBrain
- Membre Naturel
- Messages: 42
- Enregistré le: 16 Déc 2009, 21:58
-
 par SlowBrain » 03 Jan 2010, 15:38
par SlowBrain » 03 Jan 2010, 15:38
En dérivant n fois exp(ax) on obtient a^n exp(ax) donc en prenant par exemple (a1*a2*..*am) on obtient...
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 03 Jan 2010, 15:49
par barbu23 » 03 Jan 2010, 15:49
Oui, alors : :happy3:
}(x) = a_{1}^{n} e^{a_{1} x} + .. + a_{m}^{n} e^{a_{m} x} $)
Après qu'est ce qu'on fait ? :happy3:
Merci d'avance ! :happy3:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 03 Jan 2010, 15:58
par girdav » 03 Jan 2010, 15:58
En dérivant
)
on a un truc bien.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 03 Jan 2010, 15:59
par barbu23 » 03 Jan 2010, 15:59
En derivant quoi ?

De toute façon il faut se demander quant est ce que :

pour tout
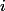
! et là, ce n'est pas trop clair pour moi ! :happy3:

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 03 Jan 2010, 16:01
par fatal_error » 03 Jan 2010, 16:01
a mon avis je pense que non :
on a
)
qui est une base.
Nous, on a f qui peut secrire
)
Pour qu'on ait
}(x) = f(x))
faut qu'on ait
 = (1,1,...,1))
cad que a_1 soit racine nieme de lunité, de même que a_m
Mais a_2 c'est une racine 2ieme de lunité et pas nieme...
Donc jpense que c'est pas possible. Mais jpeux me planter
la vie est une fête

-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 03 Jan 2010, 16:03
par barbu23 » 03 Jan 2010, 16:03
Absolument ! j'y ai pensé tout à l'heure ! mais l'idée n'est encore pas clair dans ma tête !
Plus précisement, si

, alors :
} \neq f $)
et ceçi :
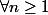
!
On peut le prouver, d'abord, pour le cas de :

, ensuite, on généralise la formule, par reccurence pour n'importe quelle
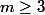
! :happy3:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 03 Jan 2010, 16:07
par girdav » 03 Jan 2010, 16:07
barbu23 a écrit:En derivant quoi ?
 f
fDe toute façon il faut se demander quant est ce que :

pour tout
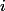
! et là, ce n'est pas trop clair pour moi ! :happy3:
Essaie donc cela, je pense que ça devrait marcher.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 03 Jan 2010, 18:56
par barbu23 » 03 Jan 2010, 18:56
Oui,mais pour me forger bien une intuition, je voudrais savoir , étant donné ,
 \in \mathbb{U}(n_1 ) \times ... \times \mathbb{U}(n_ m ) $)
:
Quelle relation y'a-t-il entre

d'un coté et

telle que :
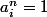
?
Est ce que c'est bien ça ?
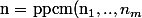 $)
Merci d'avance ! :happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités