Séries formelles

[ZLM]

Bonjour, s'il vous plaît aidez moi à résoudre cet exercice.

Exercice

Montrer que
= et que

=.

[pascal16]

je pense qu'on commence par ça :
= = = =

en posant pour n € N bn=an+1

et comme je n'ai jamais vu les série formelles et ce que le U représente, je peux pas bien aller plus loin.

[Ben314]

Salut,
Si A est un anneau commutatif unitaire, U(A) désigne le groupe (multiplicatif) des éléments inversibles de A.

Et pour répondre à "l'exercice" (qui est quasiment du cours), il suffit de connaître la définition du produit de deux séries formelles : où pour tout
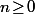
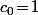
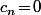
Puis, bien évidement, de regarder ça comme un système d'équations à résoudre : on connaît les et on cherche les de façon à ce que et pour tout .
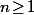
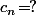
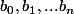
Or, comme le système est linéaire et "triangulaire" (i.e. l'équation ne contient que les inconnues ), il est trivial à résoudre et on voit immédiatement qu'il faut (et qu'il suffit) que soit inversible (i.e. qu'il soit dans ) pour qu'il y ait une solution (bien évidement unique).

[ZLM]

Bonsoir à pascal16 et à Ben314 ,
Ok. Vraiment merci beaucoup à vous deux pour l'éclaircissement. Et Encore merci beaucoup.