Bonsoir à tous ! ^_^
Durant mon marathon de sujets de concours je suis tombé sur un truc sur les séries de Fourier: Sujet CCP PC 1990 maths 1 énoncé trouvable sur : ftp://ftp.drimm.u-bordeaux1.fr/UPS/files/corriges-1990/index.html
J'ai été totalement bloquée sur la dernière partie du sujet je cherche donc des éléments de réponses voir un corrigé disponible si existant ^_^
Je suis désolée pour la forme peu pratique de ce post mais le sujet est en pdf et je ne sais pas comment le copier coller T_T. Et comme je ne maitrise absolument pas l'écriture de formules mathématiques j'ai pas pu recopier l'énoncé... Désolée T_T...
Mais bon si une gentille âme veux bien m'aider un ptit peu ^_^
Avis aux amateurs donc ^_^
Merci aux éventuelles répondeurs ^_^
Série de Fourier
8 messages
- Page 1 sur 1
Non inscrit a écrit:Bonsoir à tous ! ^_^
Durant mon marathon de sujets de concours je suis tombé sur un truc sur les séries de Fourier: Sujet CCP PC 1990 maths 1 énoncé trouvable sur : ftp://ftp.drimm.u-bordeaux1.fr/UPS/files/corriges-1990/index.html
J'ai été totalement bloquée sur la dernière partie du sujet je cherche donc des éléments de réponses voir un corrigé disponible si existant ^_^
Je suis désolée pour la forme peu pratique de ce post mais le sujet est en pdf et je ne sais pas comment le copier coller T_T. Et comme je ne maitrise absolument pas l'écriture de formules mathématiques j'ai pas pu recopier l'énoncé... Désolée T_T...
Mais bon si une gentille âme veux bien m'aider un ptit peu ^_^
Avis aux amateurs donc ^_^
Merci aux éventuelles répondeurs ^_^
Je veux bien faire un petit effort, mais pas tout le problème ! Si tu nous disais quelle question tu n'as pas su faire !
Le début...
III-1-a
x]}{2q-1})
Il est clair quex]}{2q-1}) est impair. En outre, la périodicité de la fonction sinus permet de trouver rapidement celle de
est impair. En outre, la périodicité de la fonction sinus permet de trouver rapidement celle de x]}{2q-1}) :
:
(x+T_q)=(2q-1)(x)+2\pi)
D'où :T_q = 2\pi)
ou :
 est la plus petite période de
est la plus petite période de x]}{2q-1}) . Nous savons que tous les multiples de
. Nous savons que tous les multiples de  sont également périodes de ce terme.
sont également périodes de ce terme.
Si l'on trouve une valeur qui soit période de chacun de ces n termes, cette valeur sera période de la somme. Or il est clair que toutes ces périodes ont pour multiple la plus grande d'entre elles :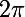 .
.
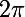 est donc période de
est donc période de  . Pour le bien, il faudrait montrer que ce nombre est bien la plus petite période, et ce n'est pas très évident : nous nous contenterons de celle-ci.
. Pour le bien, il faudrait montrer que ce nombre est bien la plus petite période, et ce n'est pas très évident : nous nous contenterons de celle-ci.
On peut donc se contenter de l'étude de entre
entre  et
et 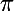 . Comme
. Comme  est impair, on peut encore réduire l'intervalle d'étude à
est impair, on peut encore réduire l'intervalle d'étude à 
On constate enfin que la propriété de la fonction sinus = sin (x)) a pour conséquence que :
a pour conséquence que :
(\pi - x)]}{2q-1}=\frac{sin[(2q-1)\pi -(2q-1)x)]}{2q-1}=\frac{sin[(2q-2)\pi +\pi -(2q-1)x)]}{2q-1}=\frac{sin[\pi -(2q-1)x)]}{2q-1}=\frac{sin[(2q-1)x)]}{2q-1})
Par conséquent = S_n(x)) ce qui montre que le graphe de la fonction est symétrique par rapport à la droite d'équation
ce qui montre que le graphe de la fonction est symétrique par rapport à la droite d'équation 
III-1-b
L'arc) de la courbe entre 0 et
de la courbe entre 0 et 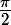 pourra donc être complété par symétrie par rapport à la droite d'équation
pourra donc être complété par symétrie par rapport à la droite d'équation  . Ensuite, une symétrie par rapport à O permettra de compléter la courbe entre
. Ensuite, une symétrie par rapport à O permettra de compléter la courbe entre  et
et . Et enfin un série de translations de vecteur
. Et enfin un série de translations de vecteur  avec
avec  définira l'intégralité de la courbe
définira l'intégralité de la courbe )
III-1-c
Pour
=\frac{\frac{1}{2n}sin(x)}{sin(\frac{x}{2n})})
est continue comme somme de fonctions continues.
Lorsque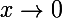 , numérateur et dénominateur sont tous deux équivalent à
, numérateur et dénominateur sont tous deux équivalent à  , donc
, donc  \to 1) , qui est la valeur de
, qui est la valeur de ) . La fonction est donc continue à droite en 0.
. La fonction est donc continue à droite en 0.
Lorsque , posons
, posons  .
.
ALors,
=sin(2n\pi - \epsilon)=sin(- \epsilon)=-sin(\epsilon))
et :
 = sin(\frac{2n\pi - \epsilon}{2n}) = sin(\pi-\frac{\epsilon}{2n})=sin(\frac{\epsilon}{2n}) \equiv \frac{\epsilon}{2n})
Donc \to -1) ce qui est la valeur de
ce qui est la valeur de ) . La fonction est donc continue à gauche en
. La fonction est donc continue à gauche en  .
.
 est donc continue sur
est donc continue sur  !
!
III-2-a
x]}{2q-1})
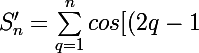x])
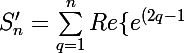xi}\})
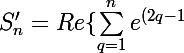xi}\})
Or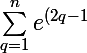xi}) est la somme des n premiers termes de la série géométrique dont le premier terme est
est la somme des n premiers termes de la série géométrique dont le premier terme est  et dont la raison est
et dont la raison est  . La somme en question est donc égale à :
. La somme en question est donc égale à :

Donc :
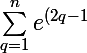xi} = e^{xi}\times \frac{[e^{2xi}]^n-1}{e^{2xi}-1}= e^{xi}\times \frac{e^{2nxi}-1}{e^{2xi}-1})
Simplifions l'expression
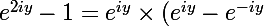 = e^{iy}*2isin(y))
On en déduit :
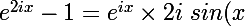)
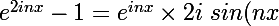)
Et :
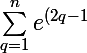xi} = e^{xi}\times \frac{e^{inx}*2i\ sin(nx)}{e^{ix}\times 2i\ sin(x)}= \frac{e^{inx}\times \ sin(nx)}{\ sin(x)})
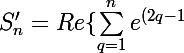xi}\})
\times sin(nx)}{sin(x)})
}{2sin(x)})
Sauf erreur...
III-1-a
Il est clair que
D'où :
ou :
Si l'on trouve une valeur qui soit période de chacun de ces n termes, cette valeur sera période de la somme. Or il est clair que toutes ces périodes ont pour multiple la plus grande d'entre elles :
On peut donc se contenter de l'étude de
On constate enfin que la propriété de la fonction sinus
Par conséquent
III-1-b
L'arc
III-1-c
Pour
est continue comme somme de fonctions continues.
Lorsque
Lorsque
ALors,
et :
Donc
III-2-a
Or
Donc :
Simplifions l'expression
On en déduit :
Et :
Sauf erreur...
Wouao ! michi michi michi !
En fait j'ai été bloquée sur presque toute la partie III mais je ne m'attendais pas à une réponse aussi complète merci beaucoup c'est déjà énorme ^_^
Je comprend déjà beaucoup mieux la méthode... Je me sens un peu gourde T_T et n'ose qu'à peine demander des petits indices pour la suite mais même quelques petites idées seront déjà bien ^_^
J'avoue que je m'attendais pas à un départ aussi détaillé merci mille fois ^_^
En fait j'ai été bloquée sur presque toute la partie III mais je ne m'attendais pas à une réponse aussi complète merci beaucoup c'est déjà énorme ^_^
Je comprend déjà beaucoup mieux la méthode... Je me sens un peu gourde T_T et n'ose qu'à peine demander des petits indices pour la suite mais même quelques petites idées seront déjà bien ^_^
J'avoue que je m'attendais pas à un départ aussi détaillé merci mille fois ^_^
Non inscrit a écrit:Wouao ! michi michi michi !
En fait j'ai été bloquée sur presque toute la partie III mais je ne m'attendais pas à une réponse aussi complète merci beaucoup c'est déjà énorme ^_^
Je comprend déjà beaucoup mieux la méthode... Je me sens un peu gourde T_T et n'ose qu'à peine demander des petits indices pour la suite mais même quelques petites idées seront déjà bien ^_^
J'avoue que je m'attendais pas à un départ aussi détaillé merci mille fois ^_^
Bon, essaie de faire le III-2-b, le III-3-a, etc... et rappelle-moi si tu bloques à nouveau, mais chacun son tour hein ?
Grroar décidément j'ai trop de mal j'abandonne... T_T je me suis totalement emmellée les pinceaux en cherchant la question III.4... T_T... petit mal de tête... T_T
Merci encore à toi Chimerade... promis la prochaine fois je ferais preuve de plus de percévérance mais là petit manque de temps... et d'aspirine ^_^
à peluche ^_^
Merci encore à toi Chimerade... promis la prochaine fois je ferais preuve de plus de percévérance mais là petit manque de temps... et d'aspirine ^_^
à peluche ^_^
Non inscrit a écrit:Grroar décidément j'ai trop de mal j'abandonne... T_T je me suis totalement emmellée les pinceaux en cherchant la question III.4... T_T... petit mal de tête... T_T
Merci encore à toi Chimerade... promis la prochaine fois je ferais preuve de plus de percévérance mais là petit manque de temps... et d'aspirine ^_^
à peluche ^_^
Ne me dis pas que j'ai fait tout ça pour rien ! Tu as passé une bonne nuit, tu t'es bourrée d'aspirine ! Allez courage, maintenant, tu reprends !
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
