Serie entiere

par **Flashtag** » 11 Jan 2020, 21:15

Soit (an) une suite de reels non nuls . On note R et R’ les rayons de convergence des séries entières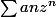

et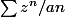

et on suppose ses rayons non nuls et finis il faut montrer que RR’>= 1 comment faire?

par **Ben314** » 11 Jan 2020, 22:20

Salut,
Si on prend

pour

pair et

pour

impair, c'est quoi le rayon de convergence de tes deux séries entières ? Conclusion.

par **Flashtag** » 17 Jan 2020, 22:26

Ok merci bcp on trouve RR'=2/3

par **Ben314** » 20 Jan 2020, 14:29

Par contre, l'inégalité contraire, à savoir

est systématiquement vraie et facile à démontrer :
Pour tout

on a

donc la série de terme général

est convergente ce qui implique en particulier que son terme général tend vers 0 et donc que

tend (en module) vers

ce qui implique que la série de terme général

est (grossièrement) divergente et donc que

.
Et le fait que

implique que

(trivial par contraposition)