Série des inverses des nombres premiers
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 22 Déc 2008, 10:57
par jeje56 » 22 Déc 2008, 10:57
Bonjour,
On notera

le nième nombre premier plus grand ou égal à 2 et soit
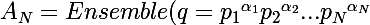)
MQ
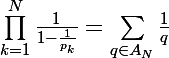
Pour N=2 : je trouve
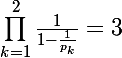
mais je n'arrive pas à calculer la somme explicitement...
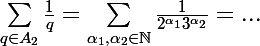
Merci bcp de votre aide !
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 22 Déc 2008, 12:07
par jeje56 » 22 Déc 2008, 12:07
Personne ?...

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 22 Déc 2008, 12:11
par fatal_error » 22 Déc 2008, 12:11
Salut,
J'ai un peu du mal a comprendre mais comme ca, je pense qu'il s'agit d'une série géométrique :
vu que
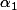
appartient a N et pareil pour
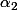
Ca revient a ecrire :
^{N+1}}{1-\frac{1}{3}})
Puis on ressort le terme.
Apres, si ya des termes qu'on saute dans N ben faut les enlever :briques:
Edit: apres réflexion j'ai ecris du cacadoum vu que \alpha c'est une valeur spécifique :marteau:
Apres double edit, en fait, N (pour les indices l et k) tend vers l'infini. Il a rien a voir avec l'indicage de Pn.
Du coup je trouve bien 3
la vie est une fête

-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 22 Déc 2008, 12:39
par jeje56 » 22 Déc 2008, 12:39
Merci à toi fatalerror, c'est bon pour le cas N=2
As-tu une piste pour le cas général ?
Merci !
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 22 Déc 2008, 12:47
par jeje56 » 22 Déc 2008, 12:47
Autant pour moi, c'est évident maintenant !

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 22 Déc 2008, 12:56
par fatal_error » 22 Déc 2008, 12:56
Ben on retrouve le produit vu qu'on peut sortir les sommes a chaque fois:
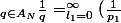^{l_1} \bigsum_{l_2=0}^{\infty} (\frac{1}{p_2})^{l_2}...\bigsum_{l_N=0}^{\infty} (\frac{1}{p_N})^{l_N}=\bigprod_{k=1}^{N} \bigsum_{l_k=0}^{\infty} (\frac{1}{p_k})^{l_k}=\bigprod_{k=1}^{N} (\frac{1}{1-\frac{1}{p_k}}))
la vie est une fête

-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 22 Déc 2008, 14:47
par jeje56 » 22 Déc 2008, 14:47
Poursuivons :
J'en déduis que :
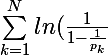\ge ln(ln(N+1)))
Puis je dois MQ la série des inverses des nombres premiers diverge...
Je butte sur cette question
Merci bcp de votre aide !

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 22 Déc 2008, 15:11
par fatal_error » 22 Déc 2008, 15:11
re,
par propriété de la croissance d'LN?
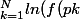)=ln(\prod f(pk))>ln(ln(N+1)))
cad
>ln(N+1)\sum \frac{1}{q}>ln(N+1))
Quand N tend vers l'infini, ca diverge
la vie est une fête

-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 22 Déc 2008, 15:44
par jeje56 » 22 Déc 2008, 15:44
Mais 1/q ne représente pas la suite des inverses des nombres premiers si ?...

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 22 Déc 2008, 19:41
par fatal_error » 22 Déc 2008, 19:41
re, oui effectivement.
Je m'étais arreté en route :marteau:
Je dirais bien que la somme de l'inverse des premiers, c'est l'ensemble des naturels(privé de 1 et 0} moins l'ensemble A_n.
Du coup, on a
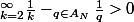
du coup, ben on a la minoration :
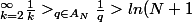)
la vie est une fête

-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 22 Déc 2008, 20:34
par ffpower » 22 Déc 2008, 20:34
Non pour conclure suffit de dire que
>1/p_k)
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 22 Déc 2008, 23:53
par _-Gaara-_ » 22 Déc 2008, 23:53
jeje56 a écrit:Puis je dois MQ la série des inverses des nombres premiers diverge...
Je butte sur cette question
Merci bcp de votre aide !
Salut,
je ne suis pas sûr mais est-ce qu'on peut tout simplement dire qu'elle est extraite de la série harmonique ? (donc a la même limite) enfin j'en sais rien

-
quinto
- Membre Irrationnel
- Messages: 1108
- Enregistré le: 01 Mai 2005, 11:00
-
 par quinto » 23 Déc 2008, 00:02
par quinto » 23 Déc 2008, 00:02
Non parce que c'est faux.
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 23 Déc 2008, 00:05
par _-Gaara-_ » 23 Déc 2008, 00:05
et pour quelles raisons =) (c'est tjrs bon de savoir nan ? )
-
quinto
- Membre Irrationnel
- Messages: 1108
- Enregistré le: 01 Mai 2005, 11:00
-
 par quinto » 23 Déc 2008, 00:07
par quinto » 23 Déc 2008, 00:07
Ce n'est pas une suite extraite.
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 23 Déc 2008, 00:13
par _-Gaara-_ » 23 Déc 2008, 00:13
Ok. Pk?
.
-
quinto
- Membre Irrationnel
- Messages: 1108
- Enregistré le: 01 Mai 2005, 11:00
-
 par quinto » 23 Déc 2008, 00:27
par quinto » 23 Déc 2008, 00:27
Evite le langage sms s'il te plait.
La raison pour laquelle ce n'est pas une suite extraite est assez claire, si tu as une extractrice disons fn et en notant Sn la série harmonique, alors fn est une suite strictement croissante d'entiers et S(fn) représente la somme de TOUS les inverses d'entiers de 1 jusqu'à fn, non ?
Une facon non triviale pour démontrer le résultat serait d'étudier la série des x^p et de regarder son rayon de convergence. Celui-ci est de 1. En utilisant le fait que toute primitive de cette série a le même rayon de convergence et que la série est à termes positifs, on doit pouvoir s'en sortir... (Si une série est à termes positifs et a 1 pour rayon de convergence, je crois que 1 est une singularité de la série).
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 23 Déc 2008, 00:30
par _-Gaara-_ » 23 Déc 2008, 00:30
D'accord, je cherchais juste à comprendre et tes phrases ultra short du début ne m'ont pas avancées ^^
Merci =)
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 23 Déc 2008, 00:35
par ffpower » 23 Déc 2008, 00:35
quinto a écrit:Evite le langage sms s'il te plait.
La raison pour laquelle ce n'est pas une suite extraite est assez claire, si tu as une extractrice disons fn et en notant Sn la série harmonique, alors fn est une suite strictement croissante d'entiers et S(fn) représente la somme de TOUS les inverses d'entiers de 1 jusqu'à fn, non ?
Une facon non triviale pour démontrer le résultat serait d'étudier la série des x^p et de regarder son rayon de convergence. Celui-ci est de 1. En utilisant le fait que toute primitive de cette série a le même rayon de convergence et que la série est à termes positifs, on doit pouvoir s'en sortir... (Si une série est à termes positifs et a 1 pour rayon de convergence, je crois que 1 est une singularité de la série).
pas du tout.Avec ca tu montrerai la divergence de la somme des 1/n².Faut forcément se servir qu on somme sur les nombres premiers...
-
quinto
- Membre Irrationnel
- Messages: 1108
- Enregistré le: 01 Mai 2005, 11:00
-
 par quinto » 23 Déc 2008, 00:35
par quinto » 23 Déc 2008, 00:35
Pas de problème.
En sommant tu vois que tu sommes les mêmes nombres que dans la série harmonique, tu les sommes juste plus vite. En fait comme ta série est à termes positifs, la facon dont tu arranges tes termes ne changera rien.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités