Série des inverses des nombres premiers
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
quinto
- Membre Irrationnel
- Messages: 1108
- Enregistré le: 01 Mai 2005, 11:00
-
 par quinto » 23 Déc 2008, 00:36
par quinto » 23 Déc 2008, 00:36
ffpower a écrit:pas du tout.Avec ca tu montrerai la divergence de la somme des 1/n².Faut forcément se servir qu on somme sur les nombres premiers...
Justement en utilisant l'argument sur les suites extraites montrer la convergence de la somme des 1/n^2.
Mon argument est correct bien que pas des plus rigoureux.
-
quinto
- Membre Irrationnel
- Messages: 1108
- Enregistré le: 01 Mai 2005, 11:00
-
 par quinto » 23 Déc 2008, 00:37
par quinto » 23 Déc 2008, 00:37
ffpower a écrit:pas du tout.Avec ca tu montrerai la divergence de la somme des 1/n².Faut forcément se servir qu on somme sur les nombres premiers...
Ok tu parlais du 2e argument ?
Pour le deuxieme argument je pense que tu as raison, j'ai parlé un peu vite.
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 23 Déc 2008, 00:46
par _-Gaara-_ » 23 Déc 2008, 00:46
je l'aimais moi mon argument de la suite extraite <3 :S
-
quinto
- Membre Irrationnel
- Messages: 1108
- Enregistré le: 01 Mai 2005, 11:00
-
 par quinto » 23 Déc 2008, 00:48
par quinto » 23 Déc 2008, 00:48
Je crois que j'ai confondu point singulier et singularité :s
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 23 Déc 2008, 10:45
par jeje56 » 23 Déc 2008, 10:45
ffpower a écrit:Non pour conclure suffit de dire que
>1/p_k)
L'inégalité n'est pas plutôt dans l'autre sens ?
Ayant montré :
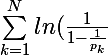\ge ln(ln(N+1)))
Ce sens ne permet pas de conclure...
Merci !
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 23 Déc 2008, 12:06
par Doraki » 23 Déc 2008, 12:06
Ben si tu la veux dans l'autre sens, tu sais que comme la dérivée de ln en 1 c'est 1, pour tout epsilon > 0, on a que pour k suffisemment grand, ln(1/(1-1/pk)) = - ln(1-1/pk) < (1+epsilon) * (1/pk)
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 23 Déc 2008, 14:04
par jeje56 » 23 Déc 2008, 14:04
Je ne comprends pas bien...
En fait on me donne l'indication :
)
(th des nombres premiers)
Je dois MQ la série
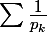
des inverses des nombres premiers diverge avec :
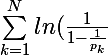\ge ln(ln(N+1)))
Merci bcp !
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 23 Déc 2008, 16:38
par ffpower » 23 Déc 2008, 16:38
euh,si t admet le thm des nomres premiers,c est direct 1/p_n est équivalant a 1/(n ln n) donc la somme des 1/p_n a meme nature que la somme des 1/(n ln n)
Si tu n admet pas le thm des nombres premiers,tu dis que 1/p_n est equivalant a ln(1/(1-1/p_n)) et tu conclus avec ce qui a été fait précédemment
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 24 Déc 2008, 10:24
par jeje56 » 24 Déc 2008, 10:24
Merci ffpower
Par la question précédente, c'est bon.
Avec l'équivalent de

, comment MQ que la série de terme général (1/n*ln(n)) diverge ?
Merci !
Edit : série de Bertrand divergente... Autant pour moi !
Merci à tous

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
