Série arctan(2/n^2)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Daniel-Jackson
- Membre Relatif
- Messages: 160
- Enregistré le: 19 Mai 2007, 17:49
-
 par Daniel-Jackson » 04 Nov 2007, 22:17
par Daniel-Jackson » 04 Nov 2007, 22:17
Salut à tous , quelqu'un aurait une idée de commentfaire pour calculer cette série de terme général
)
, pour n allant de 1 à

-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 04 Nov 2007, 22:18
par bitonio » 04 Nov 2007, 22:18
un DL par exemple ? On peut conclure en une ligne.
-
Daniel-Jackson
- Membre Relatif
- Messages: 160
- Enregistré le: 19 Mai 2007, 17:49
-
 par Daniel-Jackson » 04 Nov 2007, 22:19
par Daniel-Jackson » 04 Nov 2007, 22:19
Ah bon un DL te donne la valeur de cette série ?
Je ne cherche pas à prouver la convergence de la série (c'est triviale) mais la claculer , donne la valeur exacte de cette somme
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 04 Nov 2007, 22:21
par bitonio » 04 Nov 2007, 22:21
Autant pour moi, je lis en diagonale :) Euh, j'y réfléchis (pardon :we: )
-
Daniel-Jackson
- Membre Relatif
- Messages: 160
- Enregistré le: 19 Mai 2007, 17:49
-
 par Daniel-Jackson » 04 Nov 2007, 22:22
par Daniel-Jackson » 04 Nov 2007, 22:22
Pas de problème , toutes les pistes sont les bienvenues :happy2:
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 04 Nov 2007, 22:22
par bitonio » 04 Nov 2007, 22:22
Du coup le problème est nettement moins trivial ^^
-
Daniel-Jackson
- Membre Relatif
- Messages: 160
- Enregistré le: 19 Mai 2007, 17:49
-
 par Daniel-Jackson » 04 Nov 2007, 22:23
par Daniel-Jackson » 04 Nov 2007, 22:23
bitonio a écrit:Du coup le problème est nettement moins trivial ^^
Oui ça me casse les pieds :mur:
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 04 Nov 2007, 22:30
par bitonio » 04 Nov 2007, 22:30
T'as tenté une comparaison somme intégrale ? Ca doit bien pouvoir s'intégrer un arctan(2/n²) ?
-
Daniel-Jackson
- Membre Relatif
- Messages: 160
- Enregistré le: 19 Mai 2007, 17:49
-
 par Daniel-Jackson » 04 Nov 2007, 22:31
par Daniel-Jackson » 04 Nov 2007, 22:31
bitonio a écrit:T'as tenté une comparaison somme intégrale ? Ca doit bien pouvoir s'intégrer un arctan(2/n²) ?
Oui j'ai tenté ça mais ça n'a rien donné !
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 04 Nov 2007, 22:31
par bitonio » 04 Nov 2007, 22:31
Je regarde si j'ai plus de chance que toi...
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 04 Nov 2007, 22:33
par bitonio » 04 Nov 2007, 22:33
De toute façon on aura jamais une majoration assez fine pour avoir la valeur exacte, au mieux on aura un encadrement... Faut donc chercher autre chose...
-
Daniel-Jackson
- Membre Relatif
- Messages: 160
- Enregistré le: 19 Mai 2007, 17:49
-
 par Daniel-Jackson » 04 Nov 2007, 22:37
par Daniel-Jackson » 04 Nov 2007, 22:37
Oui je pense aussi , j'ai pensé à définir une série de fonctions et de trouver une équation différentielle simple mais non j'ai rien trouvé.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 04 Nov 2007, 22:43
par ThSQ » 04 Nov 2007, 22:43
C'est bête comme choux comme dirait mon prof !!
arctan(x) - arctan(y) = arctan((x-y)/(1+x*y))
regarder avec x=n+1 et y=n-1 :marteau: ça fait une somme télescopique et ça fait
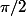
sauf erreur.
Edit: plutôt
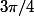
en fait
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 04 Nov 2007, 22:48
par B_J » 04 Nov 2007, 22:48
on prend plutot x=1/(n-1) et y=1/(n+1) et on obtient
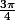
-
Daniel-Jackson
- Membre Relatif
- Messages: 160
- Enregistré le: 19 Mai 2007, 17:49
-
 par Daniel-Jackson » 04 Nov 2007, 22:53
par Daniel-Jackson » 04 Nov 2007, 22:53
Mon dieu :briques:
Merci en tout cas pour votre aide . J'avoue que j'avais pas pensé à cette formule , mais bien joué !
Bravo et ree-merci
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 04 Nov 2007, 22:59
par bitonio » 04 Nov 2007, 22:59
la honte :cry: :(
-
Daniel-Jackson
- Membre Relatif
- Messages: 160
- Enregistré le: 19 Mai 2007, 17:49
-
 par Daniel-Jackson » 04 Nov 2007, 23:09
par Daniel-Jackson » 04 Nov 2007, 23:09
bitonio a écrit:la honte


Oui on mérite d'aller au bucher :marteau:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
) , pour n allant de 1 à
, pour n allant de 1 à 
