Bonjour,
J'ai un petit exercice qui me pose problème.
Soit

un corps de caractéristique p .
Soient

et

séparable et
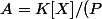)
1) Dire que vaut
)
et montrer que

est produit de r extensions finies de K et que

est K_linéaire (je rappelle c'est l'application

tel que

(p premier et A un anneau commutatif de caractéristique p)
Soit
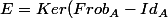 \subset A)
2) Montrer que
 = r)
3) Montrer que si

est tel que

et
 < deg (P))
alors
 = \prod_{\lambda \in K}{pgcd (P(X), Q(X)- \lambda) }) 1)
1) 
donc
= p)
= ?)
Je ne vois pas comment montrer que

est produit de r extensions finies de K
J'ai réussi à montrer que

tel que est K-linéaire.
2) Pour montrer que
 = r)
je pensais montrer que si
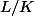
est une extension finie et

, on a
 = x \Leftrightarrow x \in K)
Soit
 = x)
c'est à dire que

mais après je ne sais pas montrer pourquoi
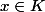 3)
3) Je n'ai réellement pas de piste
Je vous en remercie d'avance,
Cordialement
