Hilbert non séparable

[Joker62]

Hello !

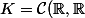On considère l'ensemble des fonctions continues de dans .

On le munit du produit scalaire défini par
On note son complété de sorte que H est un Hilbert.

On prouve sans trop de problème que la famille de fonctions est orthonormale.

J'aimerai comprendre pourquoi cela suffit à prouver que H est non séparable ?
Est-ce dû au fait que l'on a une famille orthonormale non dénombrable ?

Merci.

[mr_pyer]

Bonsoir,

Je ne sais pas quelle définition as-tu de séparable mais cela suffit en effet à démontrer que K n'est pas à base dénombrable (la définition que je prends de séparable).

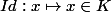
Par contre ton espace n'est pas correctement défini car la fonction pourtant ...

[Joker62]

Hello.

Merci pour la réponse.
Pour moi séparable c'est qui contient un sous-ensemble dénombrable et dense.

En fait, l'idée ça reste d'avoir une base dénombrable à priori.

Comment régler le problème de fonction Id ?

[Joker62]

À priori, il faudrait enlevé de H, toutes les fonctions qui ont une norme infinie.

Il doit y en avoir un sacré paquet :D

[mr_pyer]

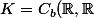En fait il faut peut-être plutôt considérer l'ensemble des fonctions continues bornées.

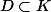
Supposons séparable, il existe dénombrable et dense dans .
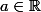
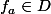
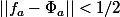
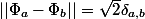
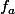
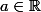
Pour tout il existe tel que . Or donc les , sont distincts, ce qui contredit la dénombrabilité de .

Voilà voilà, pas trop dur la reprise d'études ? :lol3:

[Joker62]

Parfait merci.

La reprise d'étude est très agréable en fait :)
L'enseignement m'a fait prendre beaucoup de recul et je pense que je suis davantage prêt maintenant que je ne l'étais il y a 3.

Puis c'est tellement bon l'analyse fonctionnelle :p