Bonjours, savez vous si il est possible d'utiliser la méthode de Runge-Kutta pour résoudre numériquement un système différentiel à 2 équations couplées?
Je m'intéresse au système de Fitzhugh-Nagumo.
Mais une méthode générale pour résoudre les systèmes du type:
dx/dt=f(x,y,t)
dy/dt=g(x,y,t)
avec Runge-Kutta serait parfaite.
Merci d'avance.
Runge-Kutta systèmes différentiels liés
8 messages
- Page 1 sur 1
Re: Runge-Kutta systèmes différentiels liés
Bonjour
Sans problème. Tu poses U=(x,y) et F=(f,g). Ton équation différentielle s'écrit donc U'(t)=F(U,t).
Bien sûr cette écriture est vectorielle mais la forme est la même que pour une EDO d'inconnue scalaire d'ordre 1.
Les méthodes de RK restent valables (les démonstrations de convergence aussi);, si tu transformes tes fonctions scalaires en fonctions vectorielles.
Par exemple pour la méthode RK4 classique à l'étape n
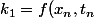 ,k_2=...)
ici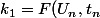=(f(x_n,y_n,t_n),g(x_n,y_,t_))) (c'est un vecteur mais à part ça mathématiquement c'est pas plus compliqué)
(c'est un vecteur mais à part ça mathématiquement c'est pas plus compliqué)
Sans problème. Tu poses U=(x,y) et F=(f,g). Ton équation différentielle s'écrit donc U'(t)=F(U,t).
Bien sûr cette écriture est vectorielle mais la forme est la même que pour une EDO d'inconnue scalaire d'ordre 1.
Les méthodes de RK restent valables (les démonstrations de convergence aussi);, si tu transformes tes fonctions scalaires en fonctions vectorielles.
Par exemple pour la méthode RK4 classique à l'étape n
ici
Re: Runge-Kutta systèmes différentiels liés
D'accord, mathématiquement je comprends le principe, mais pour le coder en python, je ne comprend pas comment procéder.
J'ai fais le programme suivant:
def rungekut(a,b,f,y0,n):
t=a
y=y0
Lt=[a]
Ly=[y0]
h=(b-a)/float(n)
for i in range (1,n+1):
k1=h*f(t,y)
k2=h*f(t+0.5*h,y+0.5*k1)
k3=h*f(t+0.5*h,y+0.5*k2)
k4=h*f(t+h,y+k3)
y=y+(1/6)*(k1+2*k2+2*k3+k4)
t+=h
Lt.append(t)
Ly.append(y)
return Lt,Ly
puis je dois définir la fonction f, mais dans le cas de mon système, je ne sais pas comment le modifier.
Merci.
J'ai fais le programme suivant:
def rungekut(a,b,f,y0,n):
t=a
y=y0
Lt=[a]
Ly=[y0]
h=(b-a)/float(n)
for i in range (1,n+1):
k1=h*f(t,y)
k2=h*f(t+0.5*h,y+0.5*k1)
k3=h*f(t+0.5*h,y+0.5*k2)
k4=h*f(t+h,y+k3)
y=y+(1/6)*(k1+2*k2+2*k3+k4)
t+=h
Lt.append(t)
Ly.append(y)
return Lt,Ly
puis je dois définir la fonction f, mais dans le cas de mon système, je ne sais pas comment le modifier.
Merci.
Re: Runge-Kutta systèmes différentiels liés
Bonjour,
je te recommande la lecture de l'ouvrage "1001 codes Python pour la modélisation", spécial classes prépas, de Lionel Uhl. La partie IV contient de nombreux codes Python pour les équations différentielles, même si ton problème n'est pas spécifiquement traité, et que les équations traitées sont "d'école" et très simples, les méthodes numériques sont bien décrites et implémentées (et d'ailleurs pas que RK), et tu trouveras sans doute de très bonnes idées et références.
je te recommande la lecture de l'ouvrage "1001 codes Python pour la modélisation", spécial classes prépas, de Lionel Uhl. La partie IV contient de nombreux codes Python pour les équations différentielles, même si ton problème n'est pas spécifiquement traité, et que les équations traitées sont "d'école" et très simples, les méthodes numériques sont bien décrites et implémentées (et d'ailleurs pas que RK), et tu trouveras sans doute de très bonnes idées et références.
Re: Runge-Kutta systèmes différentiels liés
Vous ne pouvez pas m'indiquer un programme tout fait dont je pourrais m'inspirer? Ou même réaliser le programme pour moi en me l'expliquant? Avec les équations de Fitzhugh-Nagumo?
Merci, cela m'aiderai énormément.
Merci, cela m'aiderai énormément.
Re: Runge-Kutta systèmes différentiels liés
Bonjour
En argument d'entrée, par exemple, tu ajoutes g juste après f.
Comme d'ailleurs en condition initiale y=y0 dit être remplacé par un vecteur:
y_1=y01 et y_2=y02
De même k_1=(K_11,k_12)
avec k11=f(t,y_1,y2) et K_12= g(t,y_1,y_2).
Bien sûr, si Python le permet tu écris vectoriellement.
En argument d'entrée, par exemple, tu ajoutes g juste après f.
Comme d'ailleurs en condition initiale y=y0 dit être remplacé par un vecteur:
y_1=y01 et y_2=y02
De même k_1=(K_11,k_12)
avec k11=f(t,y_1,y2) et K_12= g(t,y_1,y_2).
Bien sûr, si Python le permet tu écris vectoriellement.
Re: Runge-Kutta systèmes différentiels liés
Merci aviateur, j'ai réussi à coder mon projet.
La discussion suivante m'a également aidée:
http://www.les-mathematiques.net/phorum ... 15,1721870
La discussion suivante m'a également aidée:
http://www.les-mathematiques.net/phorum ... 15,1721870
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
