Résolution d'une équation faisant intervenir l'infini
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
balteo
- Membre Relatif
- Messages: 119
- Enregistré le: 11 Sep 2007, 15:24
-
 par balteo » 26 Nov 2009, 09:04
par balteo » 26 Nov 2009, 09:04
Bonjour,
Je suis complètement bloqué sur l'équation suivante:
60000=
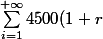^{-i})
Puis-je avoir quelques tuyaux pour la résolution d'une telle équation?
Julien.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 26 Nov 2009, 09:27
par Ben314 » 26 Nov 2009, 09:27
Bonjour,
Ne connait tu pas une formule du type
1+q+q^2+q^3+....=... ? somme finie ou infinie (avec |q|<1) ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
balteo
- Membre Relatif
- Messages: 119
- Enregistré le: 11 Sep 2007, 15:24
-
 par balteo » 26 Nov 2009, 09:39
par balteo » 26 Nov 2009, 09:39
Ben,
Si bien sûr:
1+q+q^2+q^3+q^n=(q^(n+1)-1)/(q-1)
Maintenant comment l'appliquer à des puissances négatives avec en plus une notion d'infini?
Julien.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 26 Nov 2009, 09:55
par Ben314 » 26 Nov 2009, 09:55
Les puissances "négatives" ne sont pas un problème car tu peut toujours écrire que
^{-i}=\Big({1\over 1+r}\Big)^i)
Quand au fait que la somme soit "infinie", il faut te demander, dans la formule que tu viens de me donner, ce qu'il se passe lorsque n tend vers l'infini (attention, il y a plusieurs cas selon la valeur de q...)
P.S. Attention aussi au fait que la formule que tu donne n'est valable (évidement) que pour q différent de 1 !!!!
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
balteo
- Membre Relatif
- Messages: 119
- Enregistré le: 11 Sep 2007, 15:24
-
 par balteo » 26 Nov 2009, 10:09
par balteo » 26 Nov 2009, 10:09
Ben,
Pour ce qui est des puissances négatives, j'ai pigé. Merci pour ton indication!
Par contre pour la limite et l'infini j'ai du mal: j'arrive à quelque-chose du type:
(q^(inf+1)-1)/(q-1)
????
J.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Nov 2009, 10:24
par girdav » 26 Nov 2009, 10:24
Salut.
En fait pour que la somme converge il faut que le terme que tu sommes (dans le cas particulier des séries géométriques) remplisse une certaine condition portant sur son module (ou sa valeur absolue). Vois-tu laquelle?
-
balteo
- Membre Relatif
- Messages: 119
- Enregistré le: 11 Sep 2007, 15:24
-
 par balteo » 26 Nov 2009, 10:27
par balteo » 26 Nov 2009, 10:27
Girdav,
Je ne comprends pas... :cry:
J.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Nov 2009, 10:49
par girdav » 26 Nov 2009, 10:49
En fait on peut, comme l'a dit ben314, calculer explicitement les sommes partielles (tu somme jusqu'à un certain

). Après, il faut faire tendre

vers l'infini.
Le problème que tu as souligné est en fait le problème de la limite de
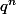
quand

tend vers l'infini.
Ceci dépend du module de

. A toi de voir quelle est la condition sur le module!
-
balteo
- Membre Relatif
- Messages: 119
- Enregistré le: 11 Sep 2007, 15:24
-
 par balteo » 26 Nov 2009, 12:46
par balteo » 26 Nov 2009, 12:46
Module veut dire valeur absolue?
Je ne vois pas du tout...
:triste:
-
balteo
- Membre Relatif
- Messages: 119
- Enregistré le: 11 Sep 2007, 15:24
-
 par balteo » 26 Nov 2009, 13:04
par balteo » 26 Nov 2009, 13:04
Quelqu'un peut-il me donner une piste svp (lien wikipedia par exemple) ou même la solution que je n'accepterai qu'après l'avoir comprise?
J.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Nov 2009, 13:46
par girdav » 26 Nov 2009, 13:46
balteo a écrit:Module veut dire valeur absolue?
Je ne vois pas du tout...
:triste:
Oui, c'est la valeur absolue si

est un nombre réel, ce qui je suppose est le cas.
Si
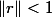
que vaut
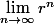
?
-
balteo
- Membre Relatif
- Messages: 119
- Enregistré le: 11 Sep 2007, 15:24
-
 par balteo » 26 Nov 2009, 14:12
par balteo » 26 Nov 2009, 14:12
Réponse:
lim = 0.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Nov 2009, 15:15
par girdav » 26 Nov 2009, 15:15
Exact. Et pour les autres cas? SI tu y arrives tu as presque résolu l'exercice.
-
balteo
- Membre Relatif
- Messages: 119
- Enregistré le: 11 Sep 2007, 15:24
-
 par balteo » 26 Nov 2009, 20:32
par balteo » 26 Nov 2009, 20:32
Ce que je ne comprends pas: dois-je me soucier des autres cas de figure?
Je sais que si on pose q=(1/(1+r)):
|q|-1 sera toujours négatif et q toujours positif car r représente un taux d'intérêt et donc la limite sera toujours égale à 0.
Que puis-je en déduire??
J.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Nov 2009, 20:34
par girdav » 26 Nov 2009, 20:34
D'accord, on a
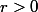
!DOnc dans ce cas il faut revenir au calcul de la somme et écrire à la place de "
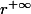
" un

, ce qui te permet de finir le calcul.
-
dudumath
- Membre Relatif
- Messages: 417
- Enregistré le: 18 Nov 2007, 11:04
-
 par dudumath » 26 Nov 2009, 21:04
par dudumath » 26 Nov 2009, 21:04
distingue le cas ou |q| < 1 , dans ce cas |q|^n tend vers 0 en l'infini,
si |q|=1, ca reste égal à 1,
si|q|=-1 ca alterne entre 1 et -1
si |q|>1, ca diverge vers +OO
-
balteo
- Membre Relatif
- Messages: 119
- Enregistré le: 11 Sep 2007, 15:24
-
 par balteo » 26 Nov 2009, 21:18
par balteo » 26 Nov 2009, 21:18
C bon j'ai compris!
On trouve: q/(1-q) et on remplace ensuite q par 1/(1+r), on trouve enfin:
r = 3/40
Merci à tous!!
:++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités