bonjour. actuellement en licence 1 maths nous étudions les fonctions hyperboliques directes et réciproques et je dois résoudre les équations suivantes :
a ch(x) + b sh(x) =0 , pour celle ci j'ai transformé ch et sh en écriture avec l'exponentielle mais ensuite je ne sais pas quoi faire ni même s'il faut trouver x ou a et b (réel)
et
(chx+shx)^(argsh(x-a)) = (chx+shx)^(argsh(x-b) pour celle ci je vois pas du tout comment on peut faire...
merci d'avance pour votre aide !
Resolution equation hyperbolique
3 messages
- Page 1 sur 1
Re: resolution equation hyperbolique
Bonjour
1) Il s'agit de résoudre l'équation en avec
avec  et
et  fixés. C'est une bonne idée de faire apparaitre
fixés. C'est une bonne idée de faire apparaitre  . Pour la suite, pose
. Pour la suite, pose 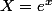 .
.
2) Est-ce bien+\cosh(x))^{\sinh^{-1}(x-a)}=(\sinh(x)+\cosh(x))^{\sinh^{-1}(x-b)}) ?
?
Si oui, il y a d'abord une étude de domaine, puis prendre le logarithme des deux membres.
1) Il s'agit de résoudre l'équation en
2) Est-ce bien
Si oui, il y a d'abord une étude de domaine, puis prendre le logarithme des deux membres.
Re: resolution equation hyperbolique
bonjour,
pour la (1):
+b sh(x)=0)
=-a ch(x))
=- \frac{a}{b}\qquad)
th=tangente hyperbolique
discuter l'existence de solutions selon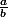 appartient à l'intervalle ]-1;1[ ou non.
appartient à l'intervalle ]-1;1[ ou non.
pour la (1):
th=tangente hyperbolique
discuter l'existence de solutions selon
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
