Fobtion trigonométrique hyperbolique
12 messages
- Page 1 sur 1
Fobtion trigonométrique hyperbolique
Bonsoir,
Je dois résoudre le système suivant:
cosh x + cosh y = 35/12
sinh x + sinh y = 25/12
J'ai beau essayer, je n'y arrive pas!...
Je dois résoudre le système suivant:
cosh x + cosh y = 35/12
sinh x + sinh y = 25/12
J'ai beau essayer, je n'y arrive pas!...
bjr,
on peut faire de la trigo hyperbolique:
+ch(q)=2 ch(\frac{p+q}{2}) ch(\frac{p-q}{2}))
+sh(q)=2 sh(\frac{p+q}{2}) ch(\frac{p-q}{2}))
en divisant membre à membre:
=\frac{5}{7})
or la tangente hyperbolique est bijective,argth s'exprime avec un log,
donc on peut considérer que la somme x+y est calculée.
En élevant au carré le système initial et en soustrayant,
avec on doit pouvoir calculer
on doit pouvoir calculer ch(y)-sh(x)sh(y)=ch(x-y))
le ch s'inverse localement sur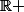 et
et  respectivement en argch() et - argch()
respectivement en argch() et - argch()
qui sont un logarithme.
On peut en déduire x-y en discutant selon son signe:
x-y >0 puis x-y < 0.
on peut faire de la trigo hyperbolique:
en divisant membre à membre:
or la tangente hyperbolique est bijective,argth s'exprime avec un log,
donc on peut considérer que la somme x+y est calculée.
En élevant au carré le système initial et en soustrayant,
avec
le ch s'inverse localement sur
qui sont un logarithme.
On peut en déduire x-y en discutant selon son signe:
x-y >0 puis x-y < 0.
Continue, tu devrais arriver à 2 couples solutions:
x = ln(3) et y = ln(2)
x = ln(2) et y = ln(3)
:zen:
je plussoie, je trouve la même chose. Maintenant, tu n'as plus que l'embarras du choix..de la méthode: expo ou trigo.
Avec exponentielle matinée de méthode algébroïde :zen: :
tu calcule
car le système s'écrit:
puis somme et produit des racines de
Merci busard_des_roseaux et Black Jack pour votre aide.
J'ai essayé le méthode des expo car je n'ai pas encore étudié la fonction tangente hyperbolique. (cependant je vais ressayer avec cette méthode dès qu'on aura fait le cours dessus car ça m'as l'air bien expliqué!..)
Mais est ce que vous pourriez détailler un peu plus car j'ai beau essayer je n'arrive pas à trouver votre résultats, je dois sûrement faire une "petite erreur" quelque part! :cry:
Merci beaucoup!
J'ai essayé le méthode des expo car je n'ai pas encore étudié la fonction tangente hyperbolique. (cependant je vais ressayer avec cette méthode dès qu'on aura fait le cours dessus car ça m'as l'air bien expliqué!..)
Mais est ce que vous pourriez détailler un peu plus car j'ai beau essayer je n'arrive pas à trouver votre résultats, je dois sûrement faire une "petite erreur" quelque part! :cry:
Merci beaucoup!
pour la modération: le code LATEX ne s'affiche pas (?)
re,
 + ( e^{ -x}+e^{ -y} ) =\frac{35}{6} \\<br />( e^x + e^y ) - ( e^{ -x}+e^{ -y} ) =\frac{25}{6} \\<br />\end{array})
Par combinaisons linéaires d'égalités:

en multipliant la seconde égalité par le facteur non nul :
:

le système initial équivaut alors à:

d'où et
et 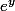 sont racines du trinôme
sont racines du trinôme 
cordialement,
:doh: :doh:
Par combinaisons linéaires d'égalités:
en multipliant la seconde égalité par le facteur non nul
le système initial équivaut alors à:
d'où
cordialement,
:doh: :doh:
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
