Bonsoir à tous, j'espère que vous allez bien !
Je viens vers vous car j'ai une question : quelle est la représentation graphique de l'expression suivante : |z-3| >= 2|z-4i|
Je ne sais pas si il vaut mieux y réfléchir directement ou développer l'expression en remplaçant z par x+yi.
J'ai essayé cette 2è méthode mais je ne vois pas la démarche à suivre.
Quelqu'un peut-il m'aider ?
Représentation graphique de |z-3| >= 2|z-4i|
6 messages
- Page 1 sur 1
Re: représentation graphique de |z-3| >= 2|z-4i|
interprétation géométrique sans prétention de donner une réponse :
|z-3| = 2|z-4i| z est deux fois plus loin de (3;0) que de (0;4)
ça sent de loin un truc du genre une hyperbole d'axe incliné
et avec <=, c'est un solide associé
|z-3| = 2|z-4i| z est deux fois plus loin de (3;0) que de (0;4)
ça sent de loin un truc du genre une hyperbole d'axe incliné
et avec <=, c'est un solide associé
Re: représentation graphique de |z-3| >= 2|z-4i|
Salut,
Par contre un autre truc trivial, c'est que ça contient pas de point "super loin" de ces deux là vu que pour un point "super loin", les deux modules sont très grand et "à peu prés égaux" dans le sens que le rapport entre les deux est à peu prés 1, donc il ne peut pas y en avoir un des deux qui vaut le double de l'autre.
Bref, c'est une conique bornée donc à priori, c'est . . .
Après, si on connaît vaguement la théorie, on sait que pour savoir la "nature" de la conique, il faut principalement regarder les coeff. devant le et le
et le 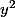 dans l'équation ce qui, dans un cas comme ici, se fait de tête et permet de déterminer la nature du bidule sans coup férir.
dans l'équation ce qui, dans un cas comme ici, se fait de tête et permet de déterminer la nature du bidule sans coup férir.
@norhvald : la méthode est bonne, mais il faut en plus avoir un minimum de connaissances pour conclure :
1) C'est quoi l'équation d'un cercle de centre) et de rayon
et de rayon  ?
?
2) C'est quoi la "mise sous forme canonique d'un trinôme du second degré ?
C'est effectivement et clairement une conique (vu que ça donne une équation de degré 2 en x et en y).pascal16 a écrit:ça sent de loin un truc du genre une hyperbole d'axe incliné
Par contre un autre truc trivial, c'est que ça contient pas de point "super loin" de ces deux là vu que pour un point "super loin", les deux modules sont très grand et "à peu prés égaux" dans le sens que le rapport entre les deux est à peu prés 1, donc il ne peut pas y en avoir un des deux qui vaut le double de l'autre.
Bref, c'est une conique bornée donc à priori, c'est . . .
Après, si on connaît vaguement la théorie, on sait que pour savoir la "nature" de la conique, il faut principalement regarder les coeff. devant le
@norhvald : la méthode est bonne, mais il faut en plus avoir un minimum de connaissances pour conclure :
1) C'est quoi l'équation d'un cercle de centre
2) C'est quoi la "mise sous forme canonique d'un trinôme du second degré ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: représentation graphique de |z-3| >= 2|z-4i|
j'en étais resté à la représentation graphique.
z est deux fois plus loin de (3;0) que de (0;4)
donc, on trace un un cercle de rayon quelconque autour de (0;4), on multiplie par 2 ce rayon et on trace le cercle autour de (3;0). Les z candidats sont à l'intersection des deux cercles quand elle existe.
(Geogebra semble tracer un cercle...)
Ceci permet de mieux voir la figure et de partir dans le bon sens (même si avec des coniques et autres, il y a des chapitres entiers qui énumèrent toutes les solutions possibles et rendent la résolution algébrique peu intéressante).
Comme dit Ben,un point loin de l'origine n'est pas candidat car |z-3| et |z-4i| sont à peu près égaux, ça donne une idée si c'est l'intérieur ou l'extérieur de la forme trouvée qui est solution de l'inéquation
z est deux fois plus loin de (3;0) que de (0;4)
donc, on trace un un cercle de rayon quelconque autour de (0;4), on multiplie par 2 ce rayon et on trace le cercle autour de (3;0). Les z candidats sont à l'intersection des deux cercles quand elle existe.
(Geogebra semble tracer un cercle...)
Ceci permet de mieux voir la figure et de partir dans le bon sens (même si avec des coniques et autres, il y a des chapitres entiers qui énumèrent toutes les solutions possibles et rendent la résolution algébrique peu intéressante).
Comme dit Ben,un point loin de l'origine n'est pas candidat car |z-3| et |z-4i| sont à peu près égaux, ça donne une idée si c'est l'intérieur ou l'extérieur de la forme trouvée qui est solution de l'inéquation
Re: représentation graphique de |z-3| >= 2|z-4i|
Si tu veut le faire de façon "plus géométrique" (*), partant de BM=k AM (en distance), tu l'écritpascal16 a écrit:j'en étais resté à la représentation graphique.
z est deux fois plus loin de (3;0) que de (0;4)
(*) Mais en fait, les calculs sont fondamentalement les mêmes.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: représentation graphique de |z-3| >= 2|z-4i|
norhvald a écrit:
Je viens vers vous car j'ai une question : quelle est la représentation graphique de l'expression suivante : |z-3| >= 2|z-4i|
Je ne sais pas si il vaut mieux y réfléchir directement ou développer l'expression en remplaçant z par x+yi.
J'ai essayé cette 2è méthode mais je ne vois pas la démarche à suivre.
la fonction carré est croissante sur
est donc équivalente à
en posant z=x+iy, on trouve, sauf erreur de calcul, l'inégalité
inéquation qui permet de déduire l'ensemble de points concerné
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
